A 2. derivált a meredekség változását adja meg. Tehát információt tudhatunk meg a függvény görbületeiről.

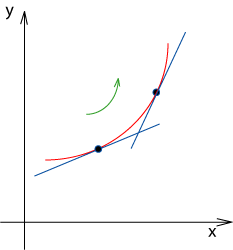
Ha f ‘(x) > 0, akkor a meredekség egyre nagyobb.
A görbe itt konvex.

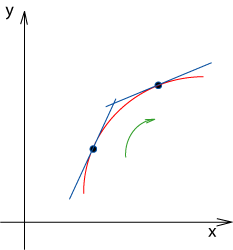
Ha f ‘(x) < 0, akkor a meredekség egyre kisebb.
A görbe itt konkáv.

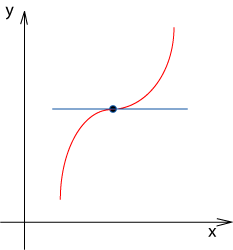
Egy inflexiós pontnál megváltozik a görbület. Ezen a helyen f ‘(x)=0.

(A biztonság kedvéért még meg kell vizsgálnunk, hogy f ‘(x) ≠ 0 teljesül-e, mert máskülönben síkpont is lehetne.)