![]()
ez azt jelenti, hogy az f(x) függvény képe alatti terület f primitív függvénye.
Példa:
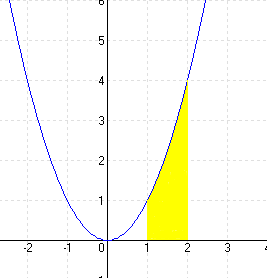
Keressük az f(x) = x² függvény grafikonja alatti területnagyságot a = 1 és b = 2 között.
![]()
primitív függvény keresése
![Rendered by QuickLaTeX.com \[ = \Bigg[ \frac{x^3}{3} \Bigg]^2_1 =\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-639c54cb07f1e5efc3ba20b3ddc49627_l3.png)
határok behelyettesítése: alsó határt a felsőből kivonni
![]()





No Comment