Egy egyenest eltolunk párhuzamosan önmagához képest.
Kitérő: Ez az egyenes a kör mellett fut el, NINCS közös pontja a körrel.
Érintő: PONTOSAN EGY közös pontja (érintőpont) van a körrel.
Szelő: KÉT KÖZÖS pontja van a körrel, illetve körvonallal.
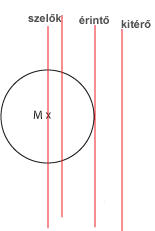
A húr középponttól való távolságát variálhatjuk. Eltolva a húrt a kör középpontjába, maximális hosszal fog rendelkezni, és ekkor átmérőnek nevezzük.
Összekötve a húr A és B végpontjait a kör középpontjával, akkor az így kapott ABM háromszög egy egyenlő szárú háromszög lesz. (Szárai a kör sugara.)
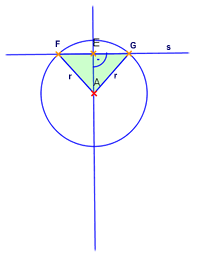
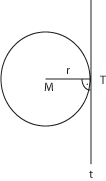
A kör érintője
- érintési pont T

- a sugár merőleges az érintőre
Szerkesztés:
- MT szakasz
- T-ben MT-hez egy merőlegest állítunk
Érintő szerkesztése P pontból
(P a körön kívül helyezkedik el)
MEP ∠ = 90°, tehát E-nek a körön és az
![]()
szakaszra mint átmérő fölé írt Thelész körön is rajta kell, hogy legyen. Az
![]()
szakasz Thalész köre a kört a keresett két érintési pontban metszi.
Kör és szög
Húrok és középponti szögek:
Minden húr két körívre bontja a kört. Összekötve a húr végpontjait a kör középpontjával, két szöget kapunk, amelyeknek csúcsa a kör középpontja. A kisebb körívhez a kisebb középponti szög tartozik, a nagyobbik körívhez a nagyobbik. Ha a húr éppen az átmérő, akkor a két körív egyenlő nagyságú csakúgy, mint a két középponti szög, ugyanis ekkor két félkörről, és két egyenes szögről van szó.
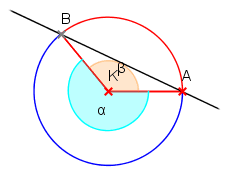
Kerületi szög – Középponti szög:
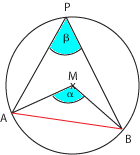 Ha a P az
Ha a P az
![]()
húrhoz tartozó köríven van, akkor az APB ∠-et kerületi szögnek nevezzük.
AMB ∠ = 2 . APB ∠ α = 2 . β
Egy kerületi szög feleakkora, mint a hozzátartozó középponti szög.
Minden egyazon húrhoz tartozó kerületi szög egyenlő nagyságú.
Körívek és körcikk:
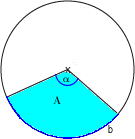 |
Körív: Körcikk: |
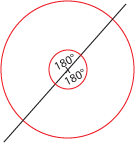
Húrnégyszögek:
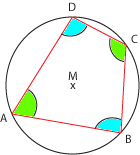
Minden húrnégyszögben a szemben lévő szögek 180°-ra egészítik ki egymást.
Szabályos n-szög:
|
Szerkesztés: |
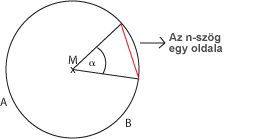 |
Példa
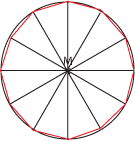
Tizenkétszög
n = 12
360° : 12 = 30°






No Comment