Az f : y = ax + b (a ; b e R) alakú függvényeket lineáris függvényeknek nevezzük.
Egy egyenes meredekségét két pont által definiáljuk: P(x1 ; y1) és Q(x2 , y2):
![\[ \frac{ y_{2} - y_{1}}{x_{2} - x_{1}}\ = \frac{\Delta y}{\Delta x} \]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-10a7931933622535501d10c081f38086_l3.png "Rendered by QuickLaTeX.com")
A Δ- Delta a „Differencia” szimbóluma.
Megmutatható, hogy:
Egy lineáris függvény képe egy k meredekségű egyenes, ami az y-tengelyt a (0 ; b) pontban metszi.
Így a függvény képe a következő módszer segítségével mindig megrajzolható:
- Rajzold be a (0;b) pontot az y-tengelyre. (b > 0 : felfele, b < 0 : lefele)
Így megkapod a függvény egyik pontját (első Pont). - Előbb nézd meg, hogy a függvény meredeksége (a) egy egész szám vagy törtszám.
- Ha a egy egész szám, akkor az első pontból kiindulva rajzolsz egy derékszögű háromszöget (meredekségi háromszög), amelynek befogója 1 (szélessége), másik befogója (magassága) éppen a > 0 : felfele, a < 0 : lefele)
Így megkapod a második Pontot. És a két pontot most már össze is lehet kötni. legyen. - Ha a egy törtszám (a = c/d), akkor az első pontból kiindulva rajzolsz egy derékszögű háromszöget (meredekségi háromszög), amelynek befogója (szélessége) d, másik befogója (magassága) éppen cc-t lefelé számolva rajzolod be, ha a tört pozitív, akkor c-t felfelé számolva rajzolod be.)
Így megkapjuk a függvény második Pontját. A két pontot pedig már össze lehet kötni. legyen. - (Ha a tört negatív, akkor
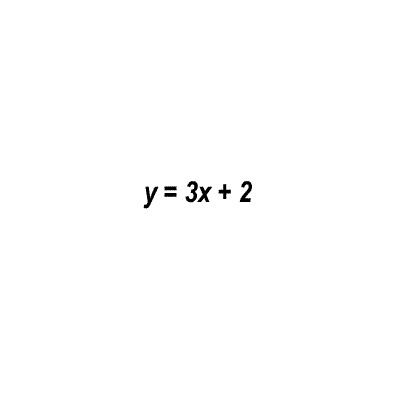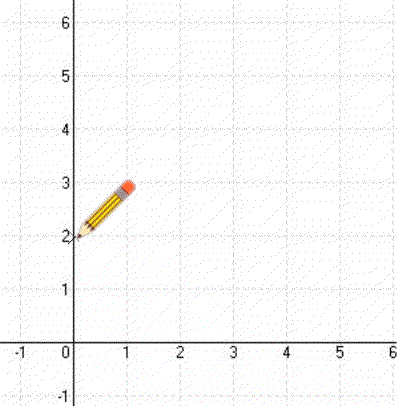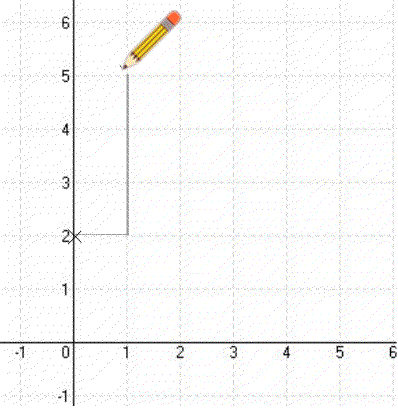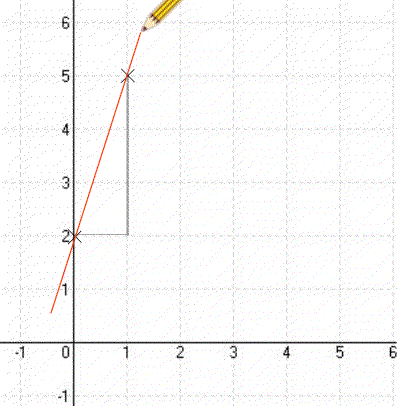
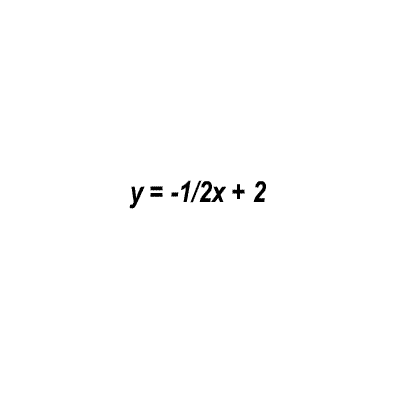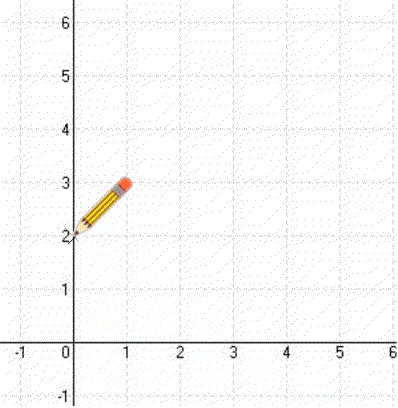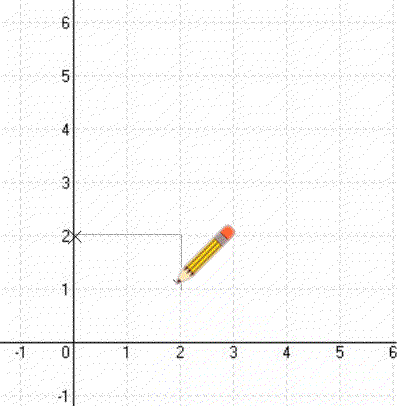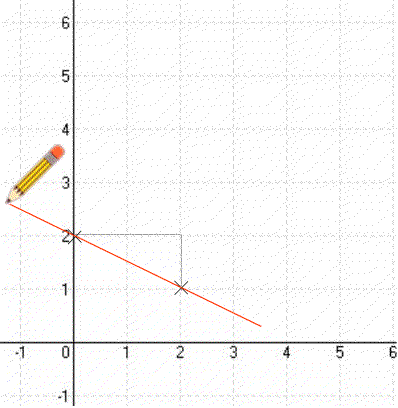
Különleges esetek
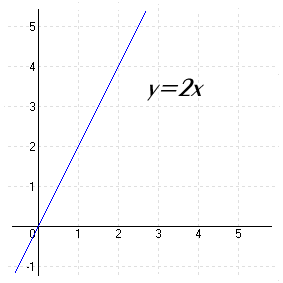
| Az y = kx függvény képe: (homogén, lineáris függvény) egy egyenes, amely átmegy az origón, és meredeksége k. |
 |
| Az y = d függvény képe : (konstans függvény) párhuzamos az x-tengellyel. |
 |
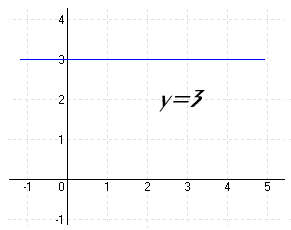Tehát a következőket állapíthatjuk meg:
| A lineáris függvény | f : y = ax + b illetve kx + b |
| képe | egyenes |
| a |
ha a > 0 monoton növekvő ha 0 > |a| < 1 |
| b | ha b < 0 negatív irányba (lefelé) b-vel az y-tengelyen
ha b > 0 pozitív irányba (felfelé) b-vel az y-tengelyen eltoljuk. |
No Comment