![\[f(x) = \frac{1}{4} * (x^3 - 3x^2 - 9x + 27)\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-f759f8ab75859988ad1ebe52f4997d1f_l3.png "Rendered by QuickLaTeX.com")
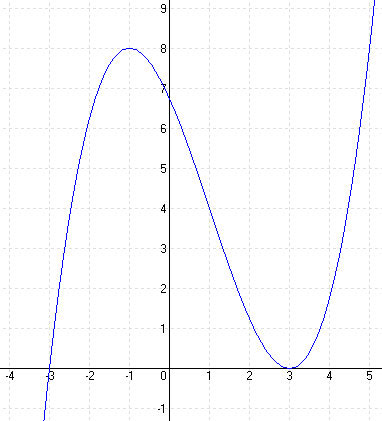
Add meg a függvény tengelyekkel való metszéspontjait, a szélsőértékeket, az inflexiós pontokat, valamint az inflexiós pontba húzott érintő egyenletét!
Megoldás:
Képezzük először a deriváltakat!
![\[f'(x) = \frac{1}{4} * (3x^2 - 6x -9)\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-c9fb3ffe1d49b19c4f0fc83d16d0e4b7_l3.png "Rendered by QuickLaTeX.com")
![\[f''(x) = \frac{1}{4} * (6x - 6)\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-e3b22d0b985d2e39459654d79945de5c_l3.png "Rendered by QuickLaTeX.com")
![\[f'''(x) = \frac{1}{4} * 6 = \frac{3}{2}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-602ddc54a01fbef081a96fe5ccb30428_l3.png "Rendered by QuickLaTeX.com")
a.) tengelyekkel való metszéspontok:
» Metszéspontok az x-tengellyel:
Zérushelyek:
f(x)=0
![\[f(x) = \frac{1}{4} * (x^3 - 3x^2 - 9x + 27) = 0 \hspace{15}\left[ \begin{array}{ccc}:\frac{1}{4}\end{array} \right]\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-34e8902fcfca675f23420567cb390bb0_l3.png "Rendered by QuickLaTeX.com")
![\[x^3 - 3x^2 - 9x + 27) = 0\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-2599b3ada8318cc540bbff16ba0c0b84_l3.png "Rendered by QuickLaTeX.com")
Horner elrendezéssel kiszámoljuk a zérushelyeket:
| Együtthatók | |||||
| x3 | x2 | x1 | x0 | ||
| Próbaszámok | 1 | -3 | -9 | 27 | Zérushelyek |
| Lehozzuk az egyet. | -1 * 1 – 3 = | -1 * -4 – 9 = | -1 * -5 + 27 = | ||
| -1 | 1 | -4 | -5 | 33 | |
| Lehozzuk az egyet. | -2 * 1 – 3 = | -2 * -5 – 9 = | -2 * 1 + 27 = | ||
| -2 | 1 | -5 | 1 | 25 | |
| Lehozzuk az egyet. | -3 * 1 – 3 = | -3 * -6 – 9 = | -3 * 9 + 27 = | ||
| -3 | 1 | -6 | 9 | 0 | -3 |
| Lehozzuk az egyet. | 0 * 1 – 3 = | 0 * -3 – 9 = | 0 * -9 + 27 = | ||
| 0 | 1 | -3 | -9 | 27 | |
| Lehozzuk az egyet. | 1 * 1 – 3 = | 1 * -2 – 9 = | 1 * -11 + 27 = | ||
| 1 | 1 | -2 | -11 | 16 | |
| Lehozzuk az egyet. | 2 * 1 – 3 = | 2 * -1 – 9 = | 2 * -11 + 27 = | ||
| 2 | 1 | -1 | -11 | 5 | |
| Lehozzuk az egyet. | 3 * 1 – 3 = | 3 * 0 – 9 = | 3 * -9 + 27 = | ||
| 3 | 1 | 0 | -9 | 0 | 3 |
Két zérushelyet találtunk:
N1 (-3; 0) N2 (3; 0)
» Metszéspontok az y-tengellyel:
x = 0
Behelyettesítünk a függvénybe:
![\[y = f(0) = \frac{1}{4} * (0^3 - 3 * 0^2 - 9 * 0 + 27) = 6,75\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-04b4c2e959d3f66c50e583b8fd779251_l3.png "Rendered by QuickLaTeX.com")
Sy (0; 6,75)
b.) Szélsőértékek: f\'(x)=0
![\[\frac{1}{4} * (3x^2 - 6x -9) = 0\hspace{15}\left[ \begin{array}{ccc}:\frac{1}{4}\end{array} \right\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-9aa53791b70e39da16269b848675e1eb_l3.png "Rendered by QuickLaTeX.com")
![\[3x^2 - 6x - 9) = 0\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-b3c356143e0a7cc2dbfeec4ed5613937_l3.png "Rendered by QuickLaTeX.com")
A megoldóképlettel megoldjuk a másodfokú egyenletet:
a = 3
b = -6
c = -9
![\[x_{1;2} = \frac {-b\pm\sqrt{b^2 - 4ac}}{2a}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-3ff9148d3ad60870a901175653b2780c_l3.png "Rendered by QuickLaTeX.com")
![\[x_{1;2} = \frac {6\pm\sqrt{-6^2 - 4 * 3 * -9}}{2 * 3} = \frac{6\pm\sqrt{36 + 108}}{6} =\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-7f7f225a1048bdb25df3baa1386b307a_l3.png "Rendered by QuickLaTeX.com")
![\[= \frac{6\pm\sqrt{144}}{6} = \frac{6\pm 12}{6} =\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-be4eb0055fc7ba3f308b3c913b2d7d73_l3.png "Rendered by QuickLaTeX.com")
![\[= \hspace{5}\nearrow \hspace{15} \frac {6 + 12}{6} = \frac {18}{6} = 3\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-a658b4133ed34cbaba738c08bd7d6174_l3.png "Rendered by QuickLaTeX.com")
![\[= \hspace{5}\searrow\hspace{15} \frac {6 - 12}{6} = \frac {-6}{6} = -1\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-cd093f4e92befe821980c2897a360df6_l3.png "Rendered by QuickLaTeX.com")
x1 = 3 x2 = -1
A hozzátartozó y értékeket megkapjuk, ha behelyettesítünk a függvénybe:
![\[y_1 = f(x_1) = \frac{1}{4} * (-1^3 - 3 * -1^2 - 9 * -1 + 27) = 8\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-53e2875bb588242216499f8bc42185e3_l3.png "Rendered by QuickLaTeX.com")
![\[y_2 = f(x_2) = \frac{1}{4} * (3^2 - 3 * 3^2 - 9 * 3 + 27) = 0\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-7cd201277f41835c19cc5c9e186ed051_l3.png "Rendered by QuickLaTeX.com")
E1 = (-1; 8) E2 = (3; 0)
Ahhoz hogy megállapítsuk, minimumról vagy maximumról van-e szó, be kell helyettesítenünk az x-et a 2. deriváltba.
![\[f''(x_1) = \frac{1}{4} * (6 * -1 - 6) = -3 \hspace{5} < 0 \hspace{3}maximum\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-9ef9a164da4b0f45315d3d374ff41f30_l3.png "Rendered by QuickLaTeX.com")
![\[f''(x_2) = \frac{1}{4} * (6 * 3 - 6) = 3 \hspace{5} > 0 \hspace{3}minimum\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-286bc6758460a48747f1a01d99eb77f0_l3.png "Rendered by QuickLaTeX.com")
max (-1; 8) min (3;0)
c.) Inflexiós pont: f”(x) = 0
![\[\frac{1}{4} * (6x - 6) = 0\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-55332b30520d27687104845a607d58a2_l3.png "Rendered by QuickLaTeX.com")
![\[6x - 6 = 0\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-9009a0607de1b0007cfa80624fea7e73_l3.png "Rendered by QuickLaTeX.com")
![\[6x = 6\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-5ff4e11d065442ef18ab6bc95759d3a9_l3.png "Rendered by QuickLaTeX.com")
![\[x = 1\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-e38b453d8c45ec1f8cd040ab2c8a4999_l3.png "Rendered by QuickLaTeX.com")
Az y-értéket megkapjuk, ha az x-et az eredeti függvénybe helyettesítjük be:
![\[y = f(x) = \frac{1}{4} * (1^3 - 3 * 1^2 - 9 * 1 + 27) = 4\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-2189a0c5c16a96e47f2075fe5328f555_l3.png "Rendered by QuickLaTeX.com")
Mivel f”(x) ≠ 0, ténylegesen inflexiós pontról van szó. W (1; 4)
Az inflexiós pontba húzott érintő egyenlete:
A meredekséget megkapjuk, ha az x-et az 1. deriváltba behelyettesítjük.
![\[k = f'(1) = \frac{1}{4} * (3 * 1^2 - 6 * 1 - 9) = -3\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-a37b0a3dcaef992b5109ca7d29d6ab31_l3.png "Rendered by QuickLaTeX.com")
Az egyenletet megadhatjuk például az
adott ponton átmenő, adott iránytangensű egyenes egyenletével.
↓
y – y1 = k . (x – x1)
(hiszen az érintő átmegy az inflexiós ponton)
y – 4 = -3 . (x – 1)
y – 4 = -3x + 3
y = -3x + 7
Most már megrajzolhatjuk a függvény képét:
No Comment