Königsberg – a mai Kalinyingrád – Leonhard Euler svájci matematikus révén vonult be a tudománytörténelembe.
A város hét hídjának elhelyezkedéséből származtatott, euleri gondolatkísérlet szolgált az első gráfelméleti probléma alapjául.
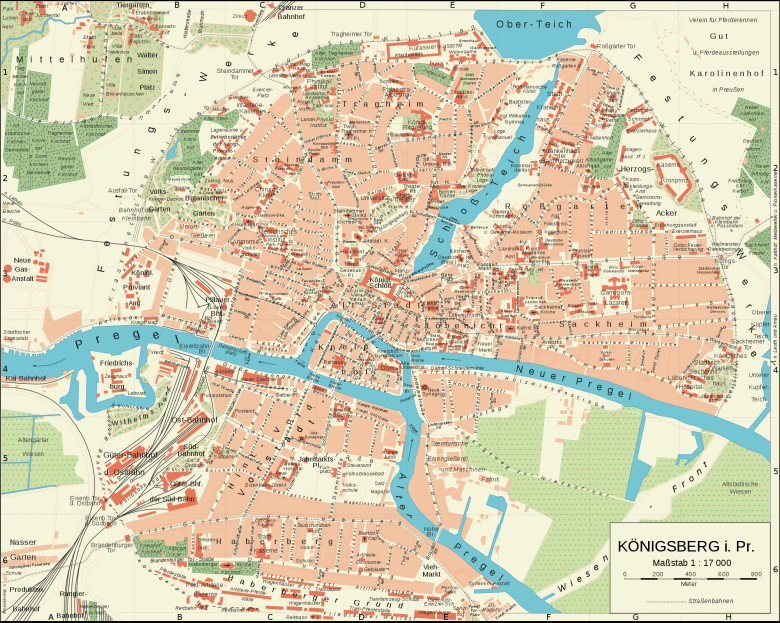
Königsberg, régi és gazdag történelmű városa a Pregel folyó két partján fekszik. Euler korában, a XVIII. század első harmadában a várost, valamint két szigetét, hét híd kötötte össze. Verőfényes délutánonként ezeken keresztül korzóztak a helyiek, vagy intézték dolgos teendőiket a hétköznapokon. Mivel a szigetek központi csomópontjait jelentették a két part közötti közlekedésnek, a hidak elhelyezkedése egy komplexebb útvonalat biztosított a város vérkeringésének. Ám a két part közvetlen összeköttetésének hiánya gondolkodóba ejtette a helyieket. Hogyan lehet végighaladni a városon és visszaérkezni a kiindulópontba úgy, hogy egy hidat ne keresztezzenek kétszer?
A feladvány megoldása sehogy sem sikerült a helyeiknek, de szerencsére kapóra jött Euler, aki ekkor a Szentpétervári Tudományos Akadémia matematikai osztályának vezetője volt. Bár Euler svájci születésű volt és 20 éves koráig ott is élt, az élete úgy hozta, hogy tanítómestere, Johann Bernoulli meghívta Oroszországba, aminek ő eleget is tett. Itt is élte le élete nagy részét, kivéve egy pár éves berlini kitérőt. Szerencséjére Oroszország ez idő tájt sikeresen vonzotta be a nagy elméket, köszönhetően a nagy péteri örökségnek és az azt követő felvilágosult abszolutizmus, akadémizmusának.
Euler nagy lelkesedéssel vágott neki a problémának. A munka kezdő időpontja nem ismert, de 1736-ban már elkészült a megoldással. Megoldása szerint nincs megoldás.
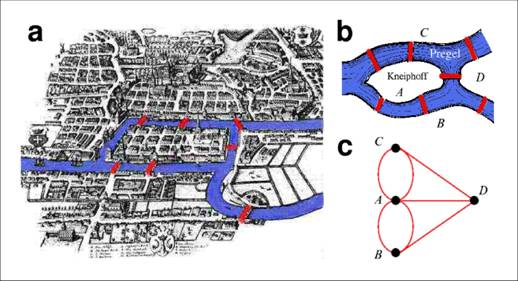
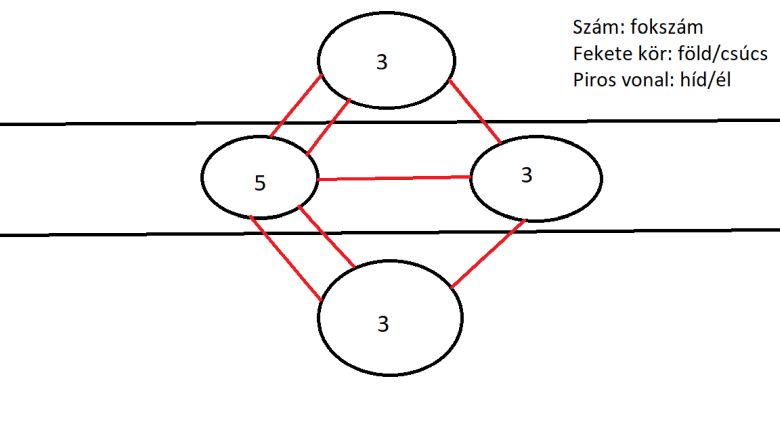
A munka közben azonban felfigyelt egy módozatra, amit ő helyek geometriájának hívott és, ami később gráfelmélet néven lett ismert. Először leírta a lehetséges útvonalakat, de ezek nem hoztak eredményt. Később rájött arra, hogy nem számít, hogy a kiindulópont a partokon, vagy a szigeteken van, vagy hogy milyen úton haladunk. Így a térkép leegyszerűsíthető oly módon, hogy a négy földdarabot egy-egy pont jelölje, amiket ő csúcsoknak nevezett el. Ezeket a csúcsokat pedig vonalak kötik össze, amit ő éleknek nevezett. Ezután minden útvonalat berajzolt az ábrájába. Így minden csúcsból a lehetséges legtöbb számú él futott ki és húzott vonalat egy másik csúcshoz.
Az így kapott ábra lehetővé tette, hogy minden csúcs fokszáma, megszámolhatóvá váljon. Ez a szám, az adott szárazföldet érintő hidak száma. Mivel a játékszabály úgy szól, hogy egy hidat a sétáló csak egyszer közelíthet meg egyik oldalról, szükségessé teszi, hogy a szárazföldre lépő egy másik hídon hagyja el azt. Vagyis az egy csúcsba befutó és onnan kifutó hidak egyértelműen megfeleltethetők egymásnak. Ez azt jelenti, hogy minden szárazföldet, páros számú hídnak kell érintenie. Kivételt csak az egész séta kezdő, illetve végpontja jelenthet. Az ábrán azonban jól látható, hogy a négy csúcs – két part, két sziget – fokszáma páratlan, mert minden csúcsból páratlan számú lehetséges útvonal rajzolódik ki a sétáló számára.
Ez a páratlanság azt okozza, hogy bármerről is induljunk, egy hidat mindenképpen kétszer kell, hogy érintsünk, viszont így a próbán megbukunk. Sajnos a valódi sétán el is fogunk bukni, mivel a probléma áthidalhatatlan, de fontosabb az út és a képlet, ami megmutatja, hogy miért.
Az Euler-út, amely minden élt csak egyszer használ, csak az alábbi két eset valamelyikében lehetséges. Az első, amikor pontosan két olyan csúcs van, amelyeknek a fokszáma páratlan. Ezek jelzik az adott csúcsból, vagyis szárazföldről való kiindulást az egyik, megérkezést a másik oldalon. Tehát a kezdőpont és a végpont különböző csúcsokban lesz, nyilvánvalóan a páratlan fokszámúakban. De ehhez szükséges, hogy az összes többi csúcs fokszáma páros legyen azért, hogy biztosítsa az áthaladást egy hídon be a szárazföldre, egy hídon pedig ki onnan. Ez nevezzük Euler-vonalnak.
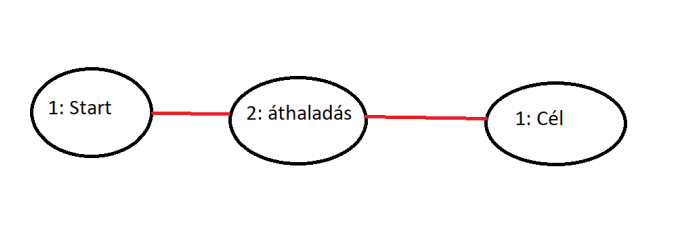A másik eset – ugyanennél a tételnél maradva – az, ha minden csúcs fokszáma páros. Ilyenkor az Euler-vonal kezdő és végpontja azonos. Tehát a sétálás startja és célpontja ugyanazon földrész lesz. Ezt Euler-körnek is nevezzük. Ugyanakkor minden Euler-kör, Euler-út is. A königsbergi hét híd elhelyezkedése tehát, kiindulva a tételből, nem eredményez olyan útvonalat, amiben a hidakat csak egyszer érintjük, köszönhetően a páratlan fokszámoknak, az összes csúcs esetében.
A matematikai probléma hipotetikusan továbbfejleszthető. Hogyan lehetne Euler-vonalat húzni a városon keresztül?
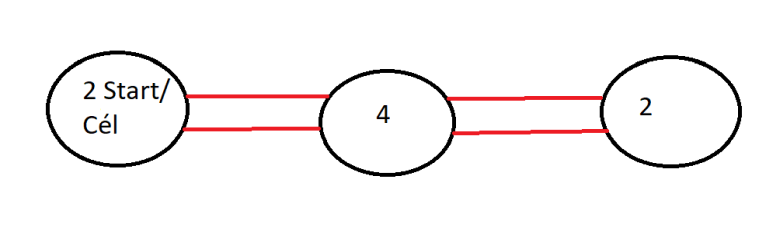
Ennek legegyszerűbb módja kiiktatni egy hidat. Ezzel a kis változtatással az egész eredeti képlet gyökeresen megváltozik. Mivel a hét híd esetében a séta során, az élekből húzott gráf nem tartalmaz sem Euler-kört, sem Euler-utat. Ha egy élt elveszünk, vagyis egy hidat felrobbantunk, akkor kapunk két csúcsot páratlan fokszámmal, kettőt párossal. Ebben az esetben teljesül az Euler-vonal. Bár ez nagyszerű fejlemény, a königsbergi hidak problematikáját nem oldja meg, mert bár egy hidat csak egyszer vett igénybe a sétáló, nem jutott vissza kiindulópontjába, hanem a másik páratlan fokszámú csúcsba. A csúcsok egyszeri érintése pedig már egy másik gráfelméleti fogalomhoz, az úgynevezett Hamilton-úthoz vezet.
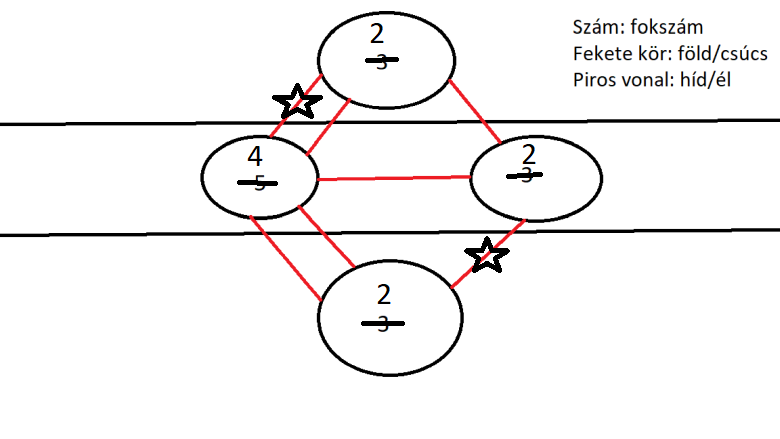Ahhoz, hogy maga a városi probléma oldódjon meg, két élt kell elvenni. De fontos úgy megvalósítani az elvételt, hogy ügyeljünk arra: mindenhol páros fokszámú csúcs maradjon. Ekkor Euler-kör képződik, vagyis visszajutásunk biztosított a startra. A történelem fintora, hogy ezt a II. világháború bevégezte a szovjet légierő hathatós közreműködésével. De az egészen biztos – bárhogy is fessen a jelenlegi Kalinyingrád –, hogy a város neve még hosszú időkig fennmarad, köszönhetően ennek a talánynak!
No Comment