1. Algebrai kifejezések összevonása
| a.) 3a + (2b – c) – (2a + 3c – b) = |
MEGOLDÁS elrejt |
| b.) 2x + 5y – (y – 3x + 2) + (x – 8) = |
MEGOLDÁS elrejt |
| c.) 3a – 8b + (11a + 4) – (5b – a + 3) = |
MEGOLDÁS elrejt |
| d.) 9 + 3e – 5f – (e + f – 1) + (7 – 4e) = | MEGOLDÁS 17 – 2e – 6f elrejt |
| e.) 2a2 + 3a – (a + 5) – (1 – 3a2) = | MEGOLDÁS 5a2 + 2a – 6 elrejt |
| f.) y3 – 6y + (2y3 + 3y – 4) = | MEGOLDÁS 3y3 – 3y – 4 elrejt |
| g.) 3x2 – y2 – (x2 – xy – y2) + (5y2 – 5xy) = | MEGOLDÁS 2x2 + 5y2 – 4xy elrejt |
| h.) 3ab + 6 + (a2 – 2ab – 5) – (4b2 – a2 +1) = | MEGOLDÁS 2a2 + ab – 4b2 elrejt |
| i.) 2 · (2a + 3b) + 3 · (3a – 2b) = | MEGOLDÁS 13a elrejt |
| j.) 6 · (a – 2b) – 2 · (a – 5b) = | MEGOLDÁS 4a – 2b elrejt |
| l.) (-4) · (2b – c + 3a) – 3 · (a + 3b – 2c) = | MEGOLDÁS 10c – 17b – 15a elrejt |
| m.) 3a · (a + 4b) + 2b · (6b – 5a) = | MEGOLDÁS 3a2 + 2ab + 12b2 elrejt |
| n.) 4m · (3n + 5) – 7n · (m + 8) = | MEGOLDÁS 5mn + 20m – 56n elrejt |
| o.) 2e · (e2 – 2ef) + f2 · (5e – 2) – 6f · (-e2 + 3ef) = |
MEGOLDÁS 2e3 – 4e2f + f2(5e-2) – 6f(-e2 + 3ef) = 2e3 – 4e2f + 5ef2 – 2f2 – 6f(-e2 + 3ef) = 2e3 – 4e2f + 5ef2 – 2f2 + 6e2f – 18ef2 = 2e3 – 13ef2 – 2f2 + 2fe2 elrejt |
| p.) (-5u) · (2u2 – uv + 3v2) + 4v · (-u2 + 3uv – 7v2) = | MEGOLDÁS -10u3 – 3uv2 + vu2 – 28v3 elrejt |
| q.) x2 · (x – 2) + x · (2x + 1) = | MEGOLDÁS x3 + x elrejt |
| r.) 2x2 · (x2 + 2x – 1) – 3x · (x2 – x + 2) = |
MEGOLDÁS 2x4 + x3 + x2 – 6x elrejt |
| s.) 4y · (y2 – 2) + 3y2 · (2y + 1) – 5 · (3 – y2) = | MEGOLDÁS 10y3 + 8y2 – 8y – 15 elrejt |
| t.) 3 · (z2 – 4z +2z) + 5z · (2z – 1) -z2 · (7 – z) = | MEGOLDÁS z3 + 6z2 – 11z elrejt |
2. Algebrai kifejezések összevonása a zárójel felbontása után
| a.) (3p + 6) · (p – 2) = | MEGOLDÁS 3p2 – 12 elrejt |
| b.) (-3p + 1) · (2 + 4p) = | MEGOLDÁS -12p2 – 2p + 2 elrejt |
| c.) (5a – 7b) · (9a -2b) = | MEGOLDÁS 45a2 – 73ab + 14b2 elrejt |
| d.) (12 + 5b) · (3b – 4a) = | MEGOLDÁS 36b + 15b2 – 48a – 20ab elrejt |
| e.) (u2 + v2) · (2u2 – v2) = | MEGOLDÁS 2u4 + u2v2 – v4 elrejt |
| f.) (3u2 – v) · (u – 4v2) = | MEGOLDÁS 3u3 – uv – 12u2v2 + 4v3 elrejt |
| g.) (g – 5h) · (2g + 3h) = | MEGOLDÁS 2g2 – 7hg – 15h2 elrejt |
| h.) (3a2 – 5a +b) · (5a – 2) = | MEGOLDÁS 15a3 – 31a2 + 10a + 5ab – 2b elrejt |
| i.) (2r2 + rs – 8s2) · (4r – 7s) = | MEGOLDÁS 8r3 – 10r2s – 39rs2 + 56s3 elrejt |
| j.) (3r2 +rs +s2) · (-4rs + s2) = | MEGOLDÁS -12r3s – r2s2 – 3rs3 +s4 elrejt |
| k.) (x2 + 5x – 2) · (2x2 – 3) = | MEGOLDÁS 2x4 + 10x3 – 7x2 – 15x + 6 elrejt |
| l.) (3a + 2) · (9a2 + 6a +4) = | MEGOLDÁS 27a3 + 36a2 + 24a + 8 elrejt |
| m.) (2a – 3b) · (-3a + b) + (4a – b) · (2a + 5b) = | MEGOLDÁS 2a2 + 29ab – 8b2 elrejt |
| n.) (2a + 3b) · (-3a + b) – (4a – b) · (2a + 5b) = | MEGOLDÁS -14a2 – 25ab + 8b2 elrejt |
| o.) (10x + 3) · (2x – 5) – (8 – 3x) · (4x + 9) = | MEGOLDÁS 32x2 – 49x – 87 elrejt |
| p.) (3r2 – s2) · (2r + 3s) + (2r – 5s) · (4r2 – 2s2) = | MEGOLDÁS 14r3 – 6rs2 – 11r2s + 7s3 elrejt |
| q.) (-3r2 – s2) · (2r + 3s) + (-2r – 5s) · (4r2 – 2s2) = | MEGOLDÁS -14r3 – 29r2s + 2rs2 + 7s3 elrejt |
| r.) (3z2 – 5z +2) · (1 – 7z) + (4z – 7) · (6z2 + z) = | MEGOLDÁS 3z3 – 26z + 2 elrejt |
| s.) (3z2 – 5z +2) · (1 – 7z) – (4z – 7) · (6z2 + z) = | MEGOLDÁS -45z3+76z2-12z+2 elrejt |
2.1 Algebrai kifejezések összevonása a zárójel felbontása után
| a.) (3a + 1)2 = | MEGOLDÁS 9a2 + 6a + 1 elrejt |
| b.) (4k + 3)2 = | MEGOLDÁS 16k2 + 24k + 9 elrejt |
| c.) (5b + 3c)2 = | MEGOLDÁS 25b2 + 30bc + 9c2 elrejt |
| d.) (x2 + 4)2 = | MEGOLDÁS x4 + 8x2 + 16 elrejt |
| e. (2x – 5)2 = | MEGOLDÁS 4x2 – 20x + 25 elrejt |
| f.) (5p – q)2 = | MEGOLDÁS 25p2 – 10pq + q2 elrejt |
| g. (a3 – a)2 = | MEGOLDÁS a6 – 2a4 + a2 elrejt |
| h.) (10ab – 2a)2 = | MEGOLDÁS 100a2b2 – 40a2b + 4a2 elrejt |
| i.) (3a + 5) . (3a – 5) = | MEGOLDÁS 9a2 – 25 elrejt |
| j.) (10x – 3z) . (10x + 3z) = | MEGOLDÁS 100x2 – 9z2 elrejt |
| k.) (r2 + 1) . (r2 -1) = | MEGOLDÁS r4 – 1 elrejt |
| l.) (7 – x) . (7 + x) = | MEGOLDÁS 49 – x2 elrejt |
| m.) (p + q)2 + (p – q)2 = | MEGOLDÁS 2p2 + 2q2 elrejt |
| n.) (3p + 2q)2 – (2p – 3q)2 = | MEGOLDÁS 5p2 + 24pq – 5q2 elrejt |
| o.) (a + 3b)2 + (3a + b) . (3a – b) = | MEGOLDÁS 10a2 + 6ab + 8b2 elrejt |
| p.) (5x + z) . (5x – z) – (2x – 5z)2 = | MEGOLDÁS 21x2 + 20xz – 26z2 elrejt |
| q.) (2a + 1) . (2a – 1) = | MEGOLDÁS 4a2 – 1 elrejt |
| r.) (2a + 1)2 – (a – 3)2 = | MEGOLDÁS 3a2 + 10a – 8 elrejt |
| s.) (c + 2d) . (c – 2d) + (c – d) . (2c + d) = | MEGOLDÁS 3c2 – cd – 5d2 elrejt |
| t.) (3x + 2) . (1 – x) – (x – 4)2 = | MEGOLDÁS -4x2 + 9x – 14 elrejt |
| u.) 5 . (y – 2)2 – 3 . (y + 2)2 = | MEGOLDÁS 2y2 – 32y + 8 elrejt |
3. Alakítsd szorzattá!
| a.) 7a2 – 14ab + 21b2 = | MEGOLDÁS 7 . (a2 – 2ab + 3b2) elrejt |
| b.) 3a2 + 6ab – 9ac = | MEGOLDÁS 3a . (a + 2b – 3c) elrejt |
| c.) 6rs – 10rt + 2r = | MEGOLDÁS 2r . (3s – 5t +1) elrejt |
| d.) 30u2v + 20v2 + 100v = | MEGOLDÁS 10v . (3u2 + 2v + 10) elrejt |
| e.) x3 – 10x2 + 50x = | MEGOLDÁS x . (x2 – 10x + 50) elrejt |
| f.) 3a4 + 5a3 – 2a2 = | MEGOLDÁS a2 . (3a2 + 5a – 2) elrejt |
| g.) 12p5 – 30p3 + 18p = | MEGOLDÁS 6p . (2p4 – 5p2 + 3) elrejt |
| h.) 16z4 – 4z2 – 12z3 = | MEGOLDÁS 4z2 . (4z2 – 1 – 3z) elrejt |
| i.) 5y2z2 + 2yz2 – yz = | MEGOLDÁS yz . (5yz + 2z – 1) elrejt |
| j.) 6a3b2 – 9ab2 – 12ab = | MEGOLDÁS 3ab . (2a2b – 3b – 4) elrejt |
| k.) x2y2z + 3x3yz + 5x2y3 = | MEGOLDÁS x2y . (yz + 3xz + 5y2) elrejt |
| l.) 2r2π + 2r2πh = | MEGOLDÁS 2rπ . (r + rh) = 2r2π . (1 + h) elrejt |
4. Alakítsd szorzattá a megadott szorzótényező szerint!
| a.) – a – 2b + 4c = (-1) . (…) | MEGOLDÁS (-1) . (a + 2b – 4c) elrejt |
| b.) 3b2 – 3a2 = (-3) . (…) | MEGOLDÁS (-3) . (-b2 + a2) elrejt |
| c.) -x3 + 3x2 + x = (-x) . (…) | MEGOLDÁS (-x) . (x2 – 3x – 1) elrejt |
| d.) 2a2b – 5ab2 – a3 = (-a) . (…) | MEGOLDÁS (-a) . (-2ab + 5b2 + a2) elrejt |
5. Alakítsd szorzattá a nevezetes azonosságok segítségével!
| a.) a2 – 25 = | MEGOLDÁS (a + 5) . (a – 5) elrejt |
| b.) b2 – 100 = | MEGOLDÁS (b + 10) . (b – 10) elrejt |
| c.) 9a2 – 25b2 = | MEGOLDÁS (3a + 5b) . (3a – 5b) elrejt |
| d.) 16c2 – 64 = | MEGOLDÁS (4c + 8) . (4c – 8) vagy 16 . (c + 2) . (c – 2) elrejt |
| e.) x4 – 9 = | MEGOLDÁS (x2 + 3) . (x2 – 3) elrejt |
| f.) a4 – b4 = | MEGOLDÁS (a2 + b2) . (a + b) . (a – b) elrejt |
| g.) x2 + 6x + 9 = | MEGOLDÁS (x + 3)2 elrejt |
| h.) a2 + 10a + 25 = | MEGOLDÁS (a + 5)2 elrejt |
| i.) y2 – 8y + 16 = | MEGOLDÁS (y – 4)2 elrejt |
| j.) z2 – 12z + 36 = | MEGOLDÁS (z – 6)2 elrejt |
| k.) 9a2 + 12ab + 4b2 = | MEGOLDÁS (3a + 2b)2 elrejt |
| l.) 100x2 – 20xy + y2 = | MEGOLDÁS (10x – y)2 elrejt |
6. Polinomok osztása
| a.) (x2 + 8x + 15) : (x + 3) = | MEGOLDÁS x + 5 elrejt |
| b.) (x2 + 4x – 12) : (x – 2) = | MEGOLDÁS x + 6 elrejt |
| c.) (x2 – 6x – 7) : (x – 4) = |
MEGOLDÁS elrejt |
| d.) (x2 – 9x + 20) : (x – 4) = | MEGOLDÁS x – 5 elrejt |
| e.) (x3 + 8x2 + 11x – 6) : (x + 6) = | MEGOLDÁS x2 + 2x – 1 elrejt |
| f.) (x3 – 8x2 + 18x – 15) : (x – 5) = | MEGOLDÁS x2 – 3x + 3 elrejt |
| g.) (6x3 – 13x2 – 18x – 5) : (2x + 1) = | MEGOLDÁS 3x2 – 8x – 5 elrejt |
| h.) (3x3 + 5x2 – 12) : (3x – 4) = | MEGOLDÁS x2 + 3x elrejt |
| i.) (x3 + 4x2 – 4x – 16) : (2x – 4) = | MEGOLDÁS 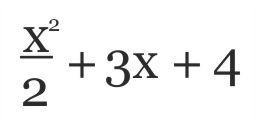 elrejt |
| j.) (x3 – 4x2 – 7x + 10) : (3x + 6) = | MEGOLDÁS 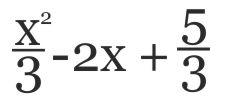 elrejt |
| k.) (x3 + 5x2 – 2x – 10) : (3x + 6) = | MEGOLDÁS x2 – 2 elrejt |
| l.) (2x3 – 3x2 + 10x – 15) : (2x – 3) = | MEGOLDÁS x2 +5 elrejt |
| m.) (x3 – 3x2 – 50) : (x – 5) = | MEGOLDÁS x2 + 2x + 10 elrejt |
| n.) (2x3 + 7x2 – 240) : (x – 4) = | MEGOLDÁS 2x2 + 15x + 60 elrejt |
| o.) (x3 – 14x – 15) : (x + 3) = | MEGOLDÁS x2 – 3x – 5 elrejt |
| p.) (x3 – 40x – 63) : (x – 7) = | MEGOLDÁS x2 + 7x + 9 elrejt |
| q.) (x3 + 27) : (x + 3) = | MEGOLDÁS x2 – 3x + 9 elrejt |
| r.) (8x3 – 1) : (2x – 1) = | MEGOLDÁS 4x2 + 2x + 1 elrejt |
| s.) (x4 – 8x2 + 16) : (x + 2) = | MEGOLDÁS x3 – 2x2 – 4x + 8 elrejt |
| t.) (x4 + x3 + 4x2 + 9x + 5) : (x2 + 2x + 1) = | MEGOLDÁS x2 – x + 5 elrejt |
| u.) (x4 + x3 – 17x2 + x + 6) : (x2 – 3x – 2) = | MEGOLDÁS x2 + 4x – 3 elrejt |
| v.) (x3 + 3x2 – 4x – 12) : (x2 – 4) = | MEGOLDÁS x + 3 elrejt |
| w.) (x4 + 6x3 – 3x2 + 12x – 10) : (x2 + 2) = | MEGOLDÁS x2 + 6x – 5 elrejt |







6k feladat sem jó szerintem,
megoldásnak 1/3x^2+x-8/3x maradék 6 -ot kaptam
a 8/3 után véletlen írtam egy x-et
Kedves tudománypláza,
Nekem a 6f feladatnál x^2+3x+4 maradék: 4 jött ki megoldásul.
Hupsz, a 6h feladatot akartam írni
Üdv,
A 3. rész L feladatában ez nem hibás?—>
2r^2*pi+2r^2*pi*h = 2r*pi(r+h)
az nem ezzel egyenlő inkább —> 2r*pi(r+rh)
Köszönjük az észrevételt. Javítottuk.
Most irtam ebből a dogából egy 2est ami TZ-volt, szoval 2db 2est ér. apukámmal gyakoroltunk és megtaláltuk ezt z oldalt. levezettem a feladatokat a füzetembe és minden jó lett. Holnap boldogan futok neki a javító dogának hála nektek. Köszönöm
(7.es vagyok szoval bocsi ha valami helytelen)
ÍGY TOVÁBB:)
Szorítunk! Örülünk, hogy segíthettünk. TP
Kedves TUDOMÁNYPLÁZA
A 2. e, feladatban nekem mínusz v a negyediken jött ki.
Máté! Igaza van. Javítottuk, köszönjük. TP
Sziasztok,
Ugy gondolom hogy a O feladat megoldasa is hibas
o.) 2e · (e2 – 2ef) + f2 · (5e – 2) – 6f · (-e2 + 3ef) =
a megoldas szerint – 6f · (-e2 + 3ef) = +6e^2f -… lesz
el tudnánekem mondni valaki hogy miert ? es miert nem +6fe^2 ?
Mert mínusz x mínusz az plusz.
Tisztelt Tudománypláza!
A 6.e feladat nekem úgy jön ki ha a második tényező +8^2
🙂 Tökéletesen igaza van
Kedves Tudománypláza!
Az 2./j.) eredmény nem (-)12r3s – r2s2 – 3rs3 +s4?
de 🙂 már nagyon megy 🙂
Kedves Szerkesztők!
Nagyon köszönöm ezt a kiváló feladatsor! Érettségire készülő diákoknak nagyszerű!
Az álábbi elírásokat találtam:
A 2.1. p) feladatban lemaradt 2x + 5z
(5x + z) . (5x – z) – (2x – 5z) helyett (5x + z) . (5x – z) – (2x – 5z)(2x – 5z)-vel jön ki a leírt megoldás.
A 3. l) feladatban 2r²π + 2r²πh = 2r²π(r + h)-ban r helyett 1 van, 2r²π + 2r²πh = 2r²π(1 + h) helyesen.
A 2. p) és q) feladat megoldása is hibás.
Eszter, nagyon figyelmes vagy. Valóban összekavarodtak ott a dolgok. Köszönjük, javítva!
Tisztelt Tudományláza!
A 6/c feladat megoldása is rosz
a helyes megoldás x-2+(-15/x-4)
Üdv
B
módosítva
Kedves Tudománypláza!
A 2/h feladat eredménye hibás +10a a helyes eredmény nem -10a, mert -x- az +
üdv
B
🙂 jogos, javítva
2, m) 2a^2+29ab-8b^2
Köszi az észrevételt, javítottuk.
Kedves Tudománypláza!
m.),p.),q.)
Üdvözlettel,
Mila
Kedves TUDOMÁNYPLÁZA!
Az alábbi feladatmegoldásában kérnék segítséget, mert nem egyértelmű sajnos a megoldása a zárójel felbontásának, illetve különböző számológépek és programok is eltérő eredményt adnak. – Hasonló példát meg találni sajnos levezetve
6:2(2+1) = 1 vagy 9 ?
48:3(4+2) = 3 vagy 96 ?
Mert szerintem az 1, illetve a 3 a helyes megoldás a zárójel felbontásának szabályai szerint
Köszönettel
Gyócsi Norbert
Kedves Norbert!
Kicsit hosszúra sikeredett a válaszadás, azért mert írtunk erről egy kis cikket. https://tudomanyplaza.hu/zarojelek-felbontasa-bonyodalom-nelkul/
Továbbá jelezzük Önnek, hogy az Ön által helyesnek vélt megoldás közül csak az egyik helyes, de mindkettőt levezettük a fentebb említett cikkben.
Üdvözlettel, a TudományPláza szerkesztősége
Kedves Tudománypláza!
Az algebrai kifejezések összevonásánál az o.) feladatban az Önök megoldása: 2e^3 – 13ef^2 – 2f^2 + 4fe^2
Szerintem azonban helyesen: 2e^3 – 13ef^2 – 2f^2 + 2fe^2
Üdvözlettel:
B. Tímea
Kedves Tímea,
tökéletesen igaza van köszönjük, a hibát javítottuk. A szerk.
Kedves Tudománypláza!
Kérhetnék egy kis magyarázatot, hogy itt a válasz utolsó tagja miért nem -4fe^2 és miért + 2fe^2, ahogy Tímea írja?
Előre is köszönöm.
Dia!
Kicsit több lépést tüntettünk fel az Ön kedvéért.
Üdv, TudományPláza
Köszönöm, így már világos.
Kedves Tudománypláza, az alábbi egyenlet összevonása hibás,
9 + 3e – 5f – (e + f – 1) + (7 – 4e) = 9 + 3e – 5f – e – f + 1 + 7 – 4e=
= 17 – 2e – 6f
Az önök megoldása ellenben a következő: 16 – 2e – 6f
Több példában is rosszul van felbontva a zárójel.
Üdvözlettel: T.Éva
Kedves Éva,
ezt a hibát javítottuk, ha talált még hibát kérjük, jelezze, mert mi egyelőre nem látunk többet.
Kedves Cikkíró!
Köszönöm szépen az oldalt, nagyon hasznos! 🙂
Szeretném megkérdezni, hogy a 3. (ALAKÍTSD SZORZATTÁ!) részben az e) feladatban a szorzattá alakítás után nem 50 marad az 5 helyett? 🙂
Köszönöm
Illetve az l) feladtban a szorzattá alakítás után nem 2r^2(1 + h) az eredmény a 2r^2(r + h) helyett?
* 2r^2π + 2r^2πh =? 2r^2π(1 + h)
Így is igaz :),mert a lehető legtöbbet emelted ki mindkét tagból. De a felhasználó neved, nem a valóságot fedi. 🙂 🙂 😉
Mindkettő helyes. Az is, amit Te írtál.
Ezt javítottuk. Jogos volt. 🙂