A gyakorlatban gyakran állunk szemben olyan feladattal, hogy egy mennyiséget (terület, felszín, térfogat, anyagfelhasználás, költség stb.) optimalizálnunk kell.

Ha a mennyiséget egy egyváltozós függvénnyel kifejezhetjük, akkor az 1. derivált segítségével kiszámíthatjuk a szélsőértéket. Ha több változó fordul elő, akkor ezeket először ki kell fejezni egy változó segítségével. 

Megoldási séma szélsőértékfeladathoz

1. Ha lehetséges, rajzoljunk egy ábrát.
2. Ismerjük fel a célfüggvényt! Mennyiség, maximálisnak, illetve minimálisnak kell-e lennie?
3. Ha több ismeretlen szerepel, mellékszámítások végzése (képletek, Pythagoras, párhuzamos szelők tétele, egy görbe egyenlete stb.).
4. Egy ismeretlent a mellékszámítások segítségével kifejezni, majd a célfüggvénybe helyettesíteni.
5. Egyszerűsítsük a célfüggvényt!
   1. Konstans szorzótényezők elhagyhatóak!
   2. A célfüggvény négyzetre emelhető (pozitív függvényértékeket figyelembe venni).
   3. Szabad a célfüggvény helyett a reciprok értéket szemlélni. (Maximum lesz a minimum és fordítva.)
6. Egyszerűsített célfüggvényt differenciálni.
7. Az 1. derivált = 0 egyenletet megoldani.
8. Ellenőrzés a 2. deriválttal.

Példa

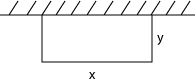
1.) Egy fal mentén egy 50 m² téglalap alakú területet kell bekeríteni. Milyen hosszúak legyenek a téglalap oldalai annak érdekében, hogy a bekerítéshez a lehető legkevesebb anyagra legyen szükség?

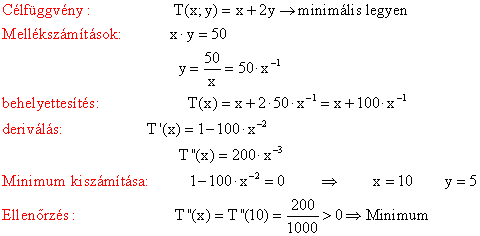
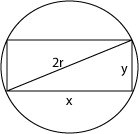
2.) Számítsuk ki, mekkorák az oldalai az r sugarú körbe írt, legnagyobb területtel rendelkező téglalapnak!

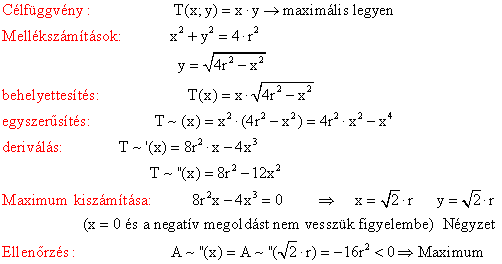
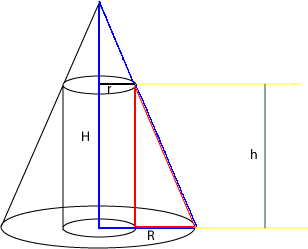
3.) Adjuk meg a legnagyobb térfogatú henger sugarát, illetve a magasságát, amelyet egy R sugarú kúpba írtunk!