Az aranymetszés

Olvasási idő: 2 perc

Az aranymetszés vagy aranyarány az arányosság egy törvénye.

A természetben és a művészetben is gyakran megjelenik, természetes egyensúlyt teremtve a szimmetria és aszimmetria között. Az aranymetszés arányait tartalmazó formák sokáig nagy esztétikai értékkel bírtak a nyugati kultúrákban, és máig alkalmazzák számos területen (például tipográfiában vagy fényképészetben). Az ókori pithagoreánusok (Pithagorasz és követői), akik szerint a valóság matematikai alapokon nyugszik, az aranymetszésben a létezés egy alaptörvényét vélték felfedezni.

Aranymetszési arányok találhatók számos ókori épületeken, középkori és reneszánsz képzőművészeti alkotásokon, de ez az arány felismerhető például az emberi testen vagy csigák mészvázán is.

Az aranyarány numerikus kifejezése az irracionális fí-szám (értéke körülbelül 1,618), mely érdekes matematikai tulajdonságokkal rendelkezik.

Matematikai definíció

Két rész az aranymetszés szerint aránylik egymáshoz, ha az egész (a + b) úgy aránylik a nagyobbik részhez (a), ahogy a nagyobbik rész (a) aránylik a kisebbik részhez (b):

$\frac{a + b}{a} = \frac{a}{b}$

Vagyis a nagyobbik fél középarányosa (mértani közepe) az egésznek és a kisebbik félnek:

a² = (a + b) ^. b

A fentiekkel egyenértékű az a megfogalmazás, hogy a nagyobbik rész úgy aránylik a kisebbik részhez, mint a kisebbik rész a két rész különbségéhez:

$\frac{a}{b} = \frac{b}{a - b}$

azaz:

b² = a ^. (a – b)

Szerkesztés útján minden vonal az aranymetszés elve szerint osztható, és hasonlóképpen a számok is. Vegyük például egészként az 1000-et. Ennek aranymetszés szerinti párja a 618.

$\frac{1000}{618} \approx \frac{618}{382}$

Ha pedig a 618-at vesszük egésznek, akkor párként a 382-t kapjuk. Tovább folytatva és a kis töredékeket elhagyva a 8 és 5, majd az 5 és 3 párokhoz jutunk. A háromhoz már nem tudunk egész párt találni. Tehát ezek a számok (8, 5 és 3) közelítőleg helyes fogalmat nyújtanak az aranymetszés osztási arányáról.

Az aranymetszés a következőképpen szerkeszthető

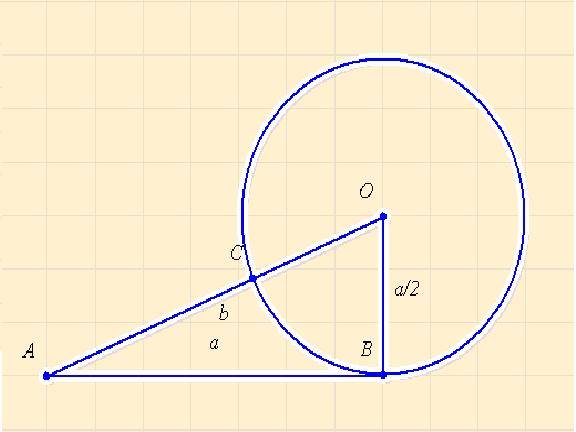
Ha az aránypárban a adott adott, akkor b is egyértelműen meghatározott, ekkor b-nek a szerkesztése a következőképpen történik. Felveszünk egy tetszőleges AB = a szakaszt, amely az aranymetszés arányai szerint a nagyobbik rész, és ehhez szerkesztjük meg az AC = b szakaszt, amely a kisebbik rész lesz. Az a szakasz B végpontjába merőleges félegyenest állítunk a-ra, erre felmérjük az a/2 távolságot. Legyen ennek végpontja az O pont. O-ból a/2 sugárral körívet húzunk, amely az AO szakaszt A-hoz közelebb eső C pontban metszi. Az AC = b távolság lesz az arány kisebbik része, ugyanis a külső pontból húzott érintő és szelőszakaszok tétele alapján:

$\frac{a}{b} = \frac{a}{a + b}$