Primitív függvények (Határozatlan integrál)
Az analízis legfontosabb részterülete az integrálszámítás. Ha a primitív függvényeket vizsgáljuk rögtön egy definícióval kezdhetjük.

Fontosabb függvények primitív függvényei
A legfontosabb elemi függvények primitív függvényei levezethetőek, de mi ezt kihagyjuk. Megtekintés: 1 320
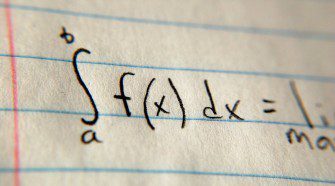
Az integrálszámítás szabályai
Példa: Egy függvény deriváltja a következő: f'(x) = 2x; A függvény átmegy a P (2; 7) ponton. P koordinátáit behelyettesítve: 22 + C = 7 ⇒ C = 3 f(x) = x2 + 3 Megtekintés: 480

A határozott integrál
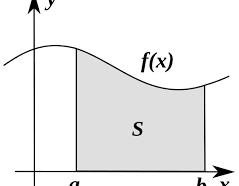
Adott az f(x) függvény; szeretnénk kiszámolni az [a; b] intervallumban a függvény és az x tengely közti területet.
A differenciál- és integrálszámítás főtétele
ez azt jelenti, hogy az f(x) függvény képe alatti terület f primitív függvénye.
Területszámítás
Figyelem: Az f(x) < 0 értékekre az integrál szintén negatív. A függvény görbéje és az x tengely közötti terület lesz az integrál. Ha a függvény a megadott intervallumon egy vagy több zérushellyel rendelkezik, akkor az egyes területeket külön-külön kell kiszámolni, majd ezeket összeadni. Ha a függvény görbéje és az x tengely közötti területet úgy kell meghatározni, …
Térfogatszámítás
Az integrál segítségével térfogatot is ki tudunk számolni. Mi itt most csak forgástestekkel fogunk foglalkozunk. Ha egy görbe az x vagy y tengely mentén forog, akkor az így előálló forgástestet vékony rétegekre lehet bontani, melyek vastagsága Dx, illetve Dy, így hengereket kapunk. A térfogatszámítás képlete hasonló az előzőekhez: forgás az x tengely mentén …


