f : y = xn
Természetes szám a hatványkitevőben
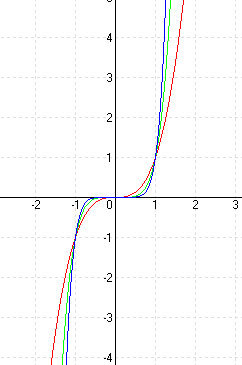
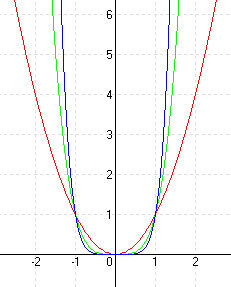
| Páratlan kitevő | Páros kitevő |
| A függvény képe egy S görbéhez hasonlít és szimmetrikus az origóra. | A függvény képe egy parabolához hasonlít és szimmetrikus az y tengelyre nézve. |
|
f3(x) = x3 |
f2(x) = x2 |
Negatív kitevők
| Páratlan kitevők | Páros kitevők |
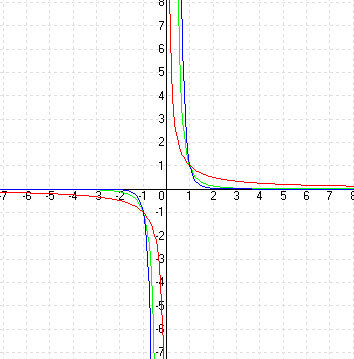
| A függvény képe hasonlít egy hiperbolához és szimmetrikus az origóra nézve. (x = 0-ra nincs értelmezve) |
A függvény képe szimmetrikus az y tengelyre nézve. (x = 0-ra nincs értelmezve) |
|
f-1(x) = x-1 |
f-2(x) = x-2 |
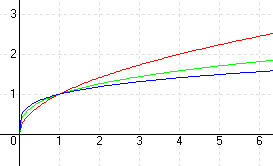
Racionális kitevők
Itt tulajdonképpen gyökfüggvényekről esik szó. Ezek a függvények csak az x > 0 tartományban értelmezhetők. A függvény képe előáll, ha a megfelelő hatványfüggvényt az 1. meridiánra tükrözzük.
piros
![\[f_\frac{1}{2}(x) = x^\frac{1}{2}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-8417c432786f3564c0e262d40770d755_l3.png "Rendered by QuickLaTeX.com")
zöld
![\[f_\frac{1}{3}(x) = x^\frac{1}{3}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-eabf571bff0c4e3e95045622650d3fc0_l3.png "Rendered by QuickLaTeX.com")
kék
![\[f_\frac{1}{4}(x) = x^\frac{1}{4}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-78131280fb4ea5097aaaed208c628f64_l3.png "Rendered by QuickLaTeX.com")
No Comment