Probléma

Keressük az f függvény változását az x helyen.

Geometriai szemléltetés

Az érintő meredeksége a P(x ; f(x)) pontban:

A P, Q pontokon átmenő szelő (zöld vonal) meredeksége:

Ezt a kifejezést nevezzük DIFFERENCIAHÁNYADOSNAK.

Minél jobban közeledik a Q pont a P ponthoz, annál meredekebb a szelő. Mikor P és Q egybeesik, a szelő és a P pontban lévő érintő (piros vonal) is egybeesik.

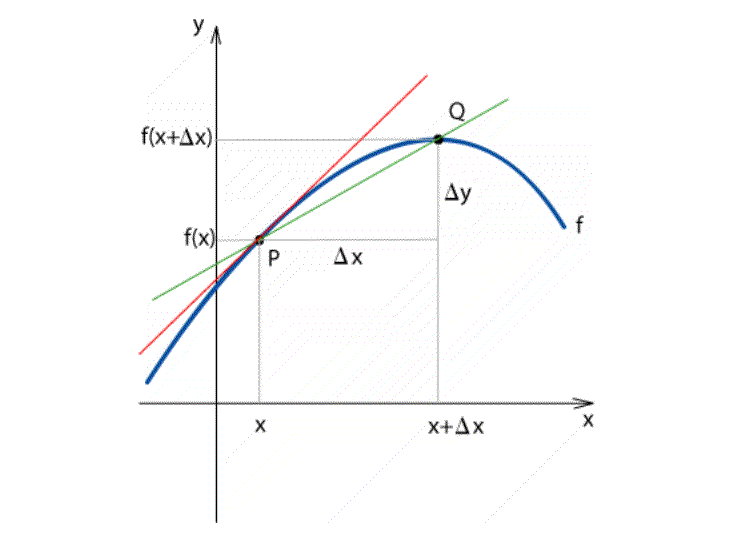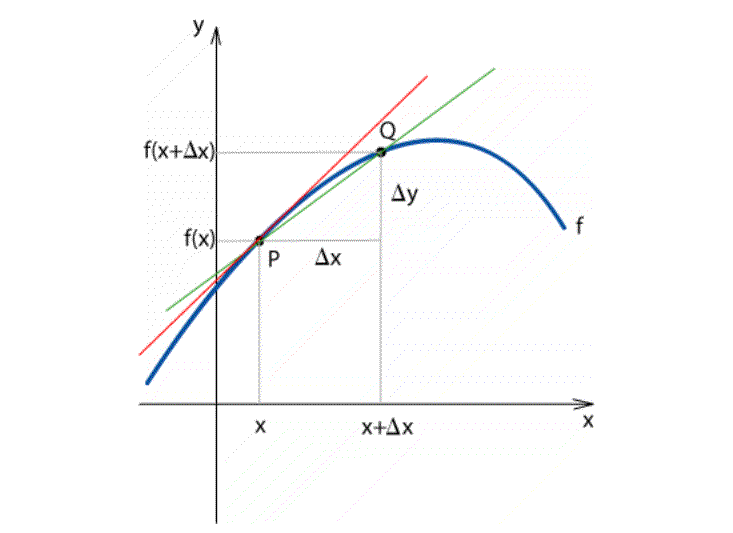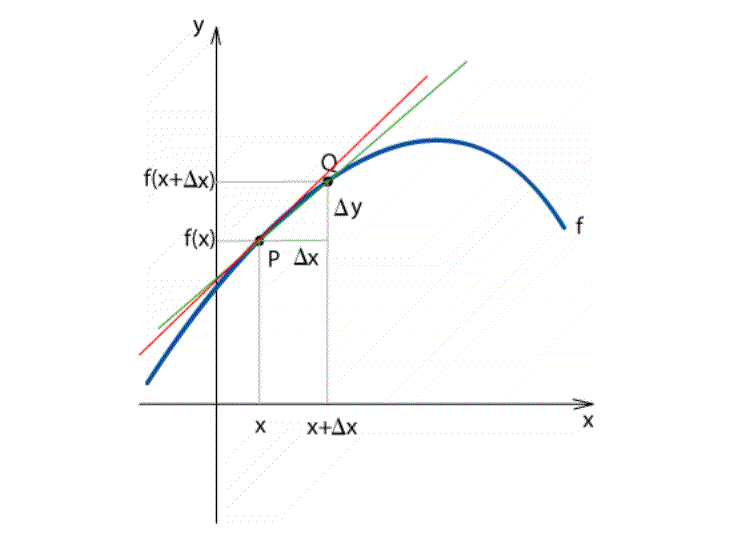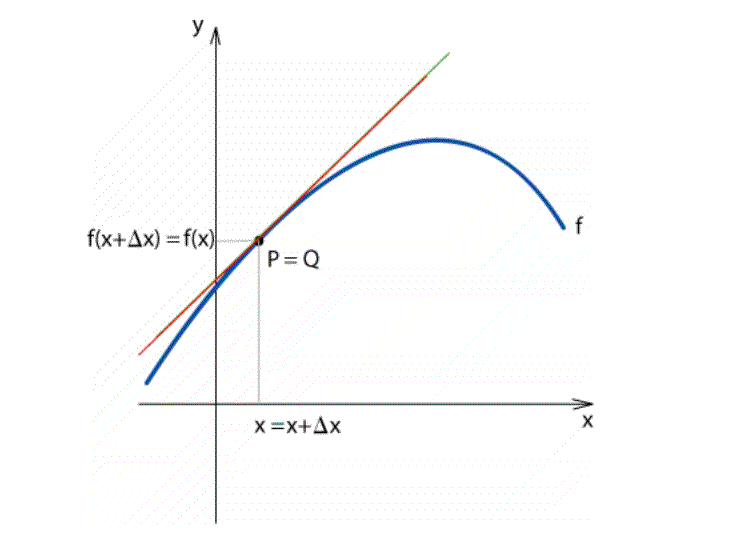
A meredekség tehát a szelő meredekségének határértéke Δx → 0 mellett. (lim = limes = határérték)

Ez az úgynevezett DIFFERENCIÁLHÁNYADOS
vagy más néven az f függvény deriváltja.

Írásmódok:

(ejtsd: „d y per d x”), f ‘(x), y’

Példa:

Keressük az érintő meredekségét az  f(x)=x² P(1;1) pontban.
A szelő meredeksége:

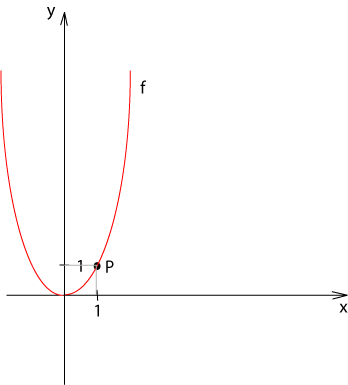
Ha Δx-szel a 0-hoz tartunk, akkor az érintő meredeksége: f ‘(1)=2

Egy tetszőleges pontban a derivált meghatározásához elegendő, az 1 helyére x-et írni: f ‘(x)=2x