A Monty Hall paradoxon – nevét egy amerikai vetélkedő (a „Let’s Make a Deal” című műsor) műsorvezetőjéről kapta – egy valószínűségi probléma.

A Monty Hall paradoxon nevű feladatba több matematika professzor bicskája is beletört már. Az alapfelvetés szerint veszünk három ajtót, amely közül kettő mögött nincs nyeremény, egy mögött viszont igen (a műsorban két kecske mellett egy sportkocsit rejtettek az ajtók).

A probléma abból fakad, hogy a választást megbonyolítják. Miután a versenyző kiválaszt egy ajtót, a műsorvezető a másik két ajtó közül kinyitja azt, ami mögött nem a nyeremény van. Ezután felteszi a kérdést:

Szeretne módosítani az eredeti választásán? Előnyére válik, ha vált?

A józan ész azt sugallja, az eredeti valószínűséget az ajtó kinyitása nem írja felül és a megmaradt két ajtóból 50% eséllyel lehet a nyereményt kiválasztani. Tehát, felesleges váltani.

Megoldás:

Akármennyire meglepő, a helyes válasz szerint igen, az esélyeink a váltás után megnőnek.

Egyértelmű, hogy amikor a játékos először választ, 1/3 valószínűséggel mutat rá a nyereményt rejtő ajtóra. Emiatt, ha nem módosít döntésén, a nyereményre való esélye 1/3 marad, ezen nem változtat az ajtó, amit a műsorvezető kinyitott. Az eredeti szituációban 2/3 valószínűséggel találtuk volna a másik két ajtó mögött a nyereményt. Ezen viszont változtat a kinyitott ajtó, ugyanis a 2/3 valószínűség akkor már úgy oszlik meg az ajtók között, hogy tudjuk az egyik mögött nincs nyeremény. Ilyen módon a 2/3 valószínűség úgymond „átszáll” a másik még becsukott ajtóra. Megéri tehát változtatni az eredeti döntésünkön, hiszen a matematika szabályai szerint az esélyeink a győzelemre pontosan megduplázódnak.

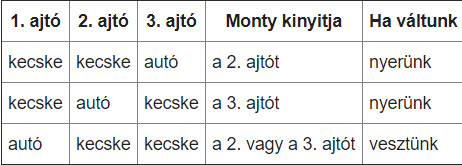
A Monty Hall paradoxon megértésben az alábbi valószínűség mátrix segíthet (feltételezve, hogy a játékos az 1. ajtót választotta először):