Közös szorzótényező kiemelése:
A disztributivitást kell alkalmazni visszafele:
Példa: 2a + 4b – 6c = 2(a + 2b – 3c)
A 2-es mint szorzótényező minden összegben szerepel, tehát kihozhatjuk a zárójel elé. Ha elvégezzük a beszorzást, akkor az eredeti kifejezést kell hogy kapjuk.
Szorzattá alakítás a nevezetes azonosságok segítségével:
Példa: 9x² + 6x + 1 = (3x + 1)²
25a² – 16b² = (5a + 4b)(5a – 4b)
Polinomok osztása:
Vesd össze a számok osztásával!
Most minden köztes lépést felírunk, még azokat is, amelyeket egyébként fejben végeznénk:
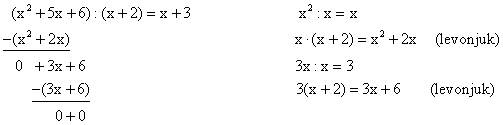







No Comment