Az élet történetét egyetlen ábrában összefoglalni az „élet fájával” szokták az utóbbi több mint másfél évszázadban.

Podani János biológus, az MTA rendes tagja szerint van tudományosan pontosabb megoldás, amely többek között kiküszöböli a nem evolúciós szemléletű osztályozási rendszert, és érzékelteti a fajgazdagságot is.

„Az élet fáját talán az élet koralljának kellene nevezni, melynek alsó ágai már nem élnek, így az átkötéseik sem láthatók.” (Charles Darwin írta 1837 vagy 1838)

A mondat nyilvánvalóan arra utal, hogy az elhalt korallágak vastag réteget képeznek az óceánban. Élő virágállatokat csak ennek tetején találunk. A metafora így egyszerre utal a kihalt és az élő fajokra. Darwin két kisméretű, egyszerű ábrával is illusztrálta gondolatát. Darwin „az élet fája” hasonlatot csak egyetlenegyszer használta az élő szervezetek közti rokonság érzékeltetésére. De e metafora éppen olyan gyakran jelenik meg a vallási szövegekben, mint a művészetben (beleértve a népművészetet) és a mitológiában.

Az élet fája, majd később a törzsfaábrázolások az utóbbi másfél száz évben terjedtek el. Az „életfa” az utóbbi három évtized biológiai kutatásainak is kedvelt eszközévé vált. Emiatt nagyon meglepő és kínos az a tény, hogy – a kémiai elemek periódusos rendszerével, a Mengyelejev-táblázattal ellentétben – nincs egzakt meghatározásunk „az élet fája” mögötti koncepcióra. Ábrázolásának módszertana sincs standardizálva, használata pedig szabadon mozog a metafora, a modell és a megértést szolgáló eszköz között.

Bizonyos típusú életfák tulajdonképpen matematikai szigorúsággal szerkesztett gráfok.

Ilyenek az úgynevezett kladogramok vagy súlyozott változataik (a filogramok, a kronogramok vagy „időfák”). A gráf diszkrét matematikai eszköz, szögpontjai valamely objektumnak – a mi esetünkben például egy fajnak – felelnek meg. A szögpontokat élek kötik össze, amelyek valamilyen kapcsolatot szimbolizálnak. Ezzel szemben állnak azon típusú ábrák, amelyek sokkal inkább hasonlítanak egy élő fára, tehát jórészt metaforikus ábrázolásnak tekinthetők.

A fent jellemzett fogalmi kavarodás, tisztázatlanság tudományos szempontból nem elfogadható, és nem szolgálja a biológiai kutatás céljait. Ez volt a kiindulópontja Podani János biológus, az MTA rendes tagja az elmúlt évtized során végzett vizsgálódásainak. 

„Félreértés ne essék, a fa típusú ábrázolások bizonyos szintig hasznosak, segítségükkel nagyon sok eredményt értünk el a szisztematikában. Ugyanakkor a fa-gráfok alkalmazásának korlátai is vannak. Amikor nagyon sok adatot kell illusztrálni, már nem működnek” – mondja Podani János.

Egy fajszintű életfa felrajzolása (tehát, amelynek szögpontjaiban az összes általunk ismert fajt feltüntetjük) az óriási adatmennyiség miatt technikailag lehetetlen feladat. Csak a jelenleg élő növényfajok bemutatása kilencpontos betűvel szedett nevekkel egy 1660 méter hosszú papírívet venne igénybe; a ma ismert körülbelül kétmillió faj fájának ábrázolásához pedig már egy 10 km hosszú papírcsík kellene.

Ha az élet fáját az élet kialakulásának történeteként értelmezzük, akkor fel kell tüntetnünk rajta a kihalt fajokat is.

Ehhez elővigyázatosan kombinálnunk kell a molekuláris és a morfológiai elemzésen alapuló kladogramokat, ami nagy kihívást jelent a kortárs biológia számára Podani János szerint. További kérdés, hogy egy fosszíliát egy bizonyos faj elődjeként vagy testvérfajaként sorolunk-e be. Mivel e kérdést csak néha-néha (vagy sohasem) tudjuk megválaszolni, egy történeti életfa megalkotása elméleti okokból eleve lehetetlen.

További, egyszerre elméleti és gyakorlati probléma, hogy a fosszíliák lajstroma rendkívül hiányos és kiegyensúlyozatlan. Az a tény, hogy napjainkig mindössze körülbelül 250 ezer kihalt faj leírásával rendelkezünk, azt bizonyítja, mennyire behatároltak az ismereteink. Annak a valószínűsége, hogy egy lágytestű élőlényről fosszília maradjon fenn, szinte a nullával egyenlő; és ne feledkezzünk meg arról sem, hogy a maradványok megtalálása mindig is szerencse kérdése lesz.

Egyes becslések szerint a valaha élt összes faj több mint 99%-a mindörökre eltűnt.

Mindebből az következik, hogy egy darwiniánus, valóban történeti jellegű, a fajokat a szögpontokban ábrázoló életfa kialakítása abszolút mértékben kizárt. Podani János javaslata szerint – bár sohasem lesz annyi információnk, hogy mindent be tudjunk mutatni – a korall típusú ábrázolásmóddal jóval inkább megragadható az a tudás, amivel a földi élet történetéről rendelkezünk. Egy koralldiagramnak mint matematikai objektumnak ugyanis a következő tulajdonságai vannak:

• Kladisztikus: feltünteti az evolúciós elágazási eseményeket.
• Kronologikus: lineáris időskálán jeleníti meg az evolúció folyamatát.
• Paleontológiai jellegű: feltünteti az ismert kihalt organizmusokat és csoportjaikat.
• Történeti jellegű: megjelenítheti a jelentős makroevolúciós és a geológiai eseményeket.
• Önhasonló: a diagramra rá lehet nagyítani a részletekért.
• Folytonos (matematikai értelemben): mentes a diszkrét matematika, a gráfelmélet korlátaitól. A korall mint elágazásairól nevezetes geometriai alakzat pontjait többek között egyedként, populációként vagy taxonként is meghatározhatjuk.
• Horizontális események is bemutathatók rajta, mint például a hibridizáció vagy az endoszimbiózis.
• Rangmentes: a csoportok elkülönítésében kiküszöböli a nem evolúciós szemléletű osztályozási rendszert, és a korall ágait tekinti taxonómiai egységeknek.
• Érzékelteti a sokféleséget: a fajgazdagságot minden csoport esetén ugyanabban a léptékben ábrázolja, így látható, hogyan oszlik meg közöttük a diverzitás.

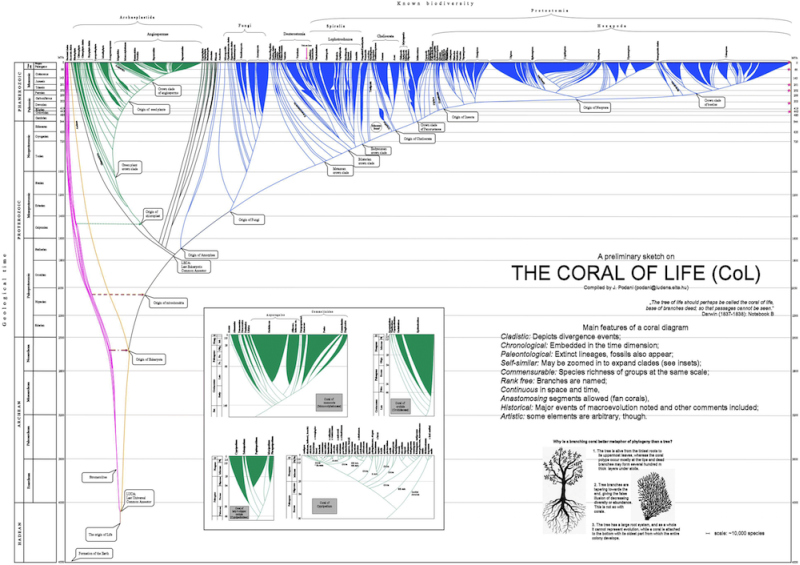
Az új típusú ábrázolás elágazási mintázata megegyezik egy fáéval, azonban a szögpontokat és az éleket síkidomok váltják fel. A korall egyébként mint metafora is alkalmasabb a fánál az evolúció bemutatására, mert az előbbi egy kis méretű telepből növekszik függőleges irányban felfelé, majd később ágazik el. Ezzel szemben a magról fejlődő fa két irányba (gyökérzet, korona) nő, s a gyökérzet ugyanolyan komplex struktúra, mint a korona. Továbbá a fa ágainak átmérője fokozatosan csökken, míg a korall felső részei akár vastagabbak is lehetnek, mint az alsók, így jobban szimbolizálják a fajgazdagság ingadozásait. A fák ágai sosem egyesülnek, míg a korallágak újra összeolvadhatnak (anasztomózisok).

A korall segítségével a horizontális evolúciós események is bemutathatók.

„A korall típusú ábrázolás a nagy adatmennyiség problémáját is rugalmasan kezeli. Amit a fa típusú ábrázoláson sok szögpontként jelenítünk meg, azt a korallon egy síkidomként ábrázoljuk. Így például a bogarak sokszor csak egyetlenegy szögpontként szerepelnek az élet fáján, s elvész a sokféleségre vonatkozó információ. A korall-ábrán viszont nagyon szépen látható, hogy a legtöbb faj az ízeltlábúakhoz tartozik, és a fajgazdagság időbeli változása is bemutatható. Ez gráfokkal egyszerűen nem megy, néhány ezer, tízezer vagy annál is több szögponttal lehetetlen jól áttekinthető rajzot készíteni” – mondja Podani János.

Az ábrázolásmód hátránya, hogy végső soron a korallt csak kézzel lehet megrajzolni. Az ábra sok kladisztikai, paleontológiai, geológiai ismeretanyag és főleg molekuláris biológiai eredmények egyesítésével készül. Így az ábraszerkesztés összességében nem írható le matematikailag, teljességében nem algoritmizálható. Az ábrának van művészi vetülete is, vagyis az adatok hiányát szubjektív módon kell pótolni – például sohasem fogjuk megtudni, hogy 100 millió évvel ezelőtt hány madárfaj létezett, sőt a ma élő madárfajok számáról sincs teljesen pontos információnk, nem beszélve a rovarokról és a puhatestűekről.

„Arra valószínűleg lehetne írni egy internetes applikációt, hogy az ábra egy részletére kattintva az kinagyítva jelenjen meg, majd annak bármely finomabb részlete tovább nagyítható legyen.”

A rajz egy sokak által nem feltétlenül kedvelt tudományterületet, a rendszertant is jelentősen befolyásolhatja.

„A biológiai rendszertan átalakulóban van, a linnéi alapokon nyugvó, tradicionális felfogás nem húzható rá egy térben és időben egyformán értelmes osztályozásra. Ez semmit sem von le Carl Linné zsenialitásából, hiszen az ő idejében, a 18. században, még szinte mindenki a fajok állandóságáról beszélt.”

Podani János azt az elvet képviseli, miszerint el kellene hagynunk a „család”, „osztály”, „rend” és hasonló kategóriákat (a rangokat),

és a filogenetikai rendszerezés eredményeit kellene minél szélesebb körben használnunk. (A korall típusú ábrán, mint említettük, a kisebb-nagyobb ágak felelnek meg egy taxonómiai csoportnak.)

Mai szemmel nézve a genus (nemzetség) mint faj feletti kategória is elavult fogalom, csak az a fő gond, hogy a genusnév benne van a szervezetek kettős nevében, a fajt jelölő részt megelőzve.

„Szinte lehetetlen vállalkozás lenne ezeket is mind lecserélni. Érdekes módon, ha valaki például a biokémia területén fedez fel valami újat, az hamar elterjed, s mindenki elfelejti a korábbi, esetleg teljesen hibás állításokat. A taxonómia berkeiben azonban nagyon nehezen megy a változtatás” – teszi hozzá Podani János.

Aki tanulmányát éppen azért publikálta open access módon, a leglazább Creative Commons licenc keretében, hogy sokak további munkájához jelenthessen kiindulópontot. A licenc lehetővé teszi, hogy a cikket és annak ábráit bárki megoszthassa, így szabadon másolhatja, terjesztheti és át is dolgozhatja – azzal a feltétellel, hogy a szerzőre megfelelő módon hivatkozik, és jelzi, ha a művön változtatást hajtott végre.

Forrás: https://link.springer.com/article/10.1007/s11692-019-09474-w