Az agyban a szürkeállomány tartalmazza az idegsejtek, a neuronok sejttestjeit (szómáit), a fehérállomány pedig egy zsírszerű anyaggal, a mielinnel szigetelt axonkötegeket, azaz az idegsejtek nyúlványait.

Jó ideje ismert, hogy a homloklebeny jobb felében a fehérállomány nagyobb térfogatú, mint a bal oldalon, így azt hihetnénk, hogy ott több kapcsolat van az idegsejtek között. Az ELTE kutatói azonban meglepő eredményre jutottak.

Az ELTE PIT Bioinformatikai Csoportjának kutatói, Szalkai Balázs doktorjelölt, Varga Bálint doktorandusz és Grolmusz Vince professzor most kimutatták, hogy – a várakozásokkal ellentétben – a bal homloklebenyben statisztikailag szignifikánsan több és – matematikailag jól meghatározott értelemben – „jobb” kapcsolat van az idegsejtek között, mint a jobb homloklebenyben.

Hasonlóan tanulmányozták a halántéklebeny és a fali lebeny belső kapcsolatait. Ezekben a lebenyekben nem a bal oldali (mint a homloklebenyben), hanem a jobboldali kapcsolatból van több, és ezek a kapcsolatok „jobbak” is, több komplex mérték szerint. Ez is eléggé meglepő, mert általában a baloldali halántéklebeny nagyobb, így azt várhatnánk, hogy ott gazdagabbak a kapcsolatok. Az ELTE kutatói többek között a minimális lefogó pontrendszer elemszámát hasonlították össze a lebenyek között.

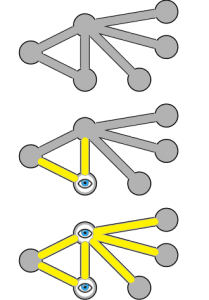
Példa a minimális lefogó pontrendszerre. Olyan csúcsokat kell találni, amelyekből kiinduló élek már az összes élet lefogják (ez a lefogó pontrendszer), és az ilyen lefogó pontrendszerek közül a legkisebb elemszámút keressük (ez a minimális lefogó pontrendszer). A felső ábra a gráf, amelynek éleit le szeretnénk fogni. A középső ábrán a szemmel jelzett csúcs csak a sárga éleket fogja le, ez még nem lefogó pontrendszer.

A minimális lefogó pontrendszer elemszáma jól alkalmazható a gráfok bonyolultságának leírására. Ha ez az érték nagy, akkor a gráf bonyolultabb, gazdagabb összeköttetésekkel rendelkezik, ha alacsonyabb, akkor ennek az ellenkezőjét gondoljuk.

Például az n csúcsú teljes gráfban, ahol minden csúcs az összes többivel össze van kötve, ez az érték n-1, az üres n-csúcsú gráfban (amelynek egy éle sincs) ez az érték 0. Nagyobb, azaz több csúcsú gráfban várható, hogy ez az érték is nagyobb, ezért gyakran nézik a minimális lefogó pontrendszer elemszámának normált változatát, azaz amikor leosztjuk a gráf csúcsszámával ezt az értéket.

A kutatók azt találták, hogy a bal homloklebeny nemcsak több élt tartalmaz, hanem még a normál minimális lefogó pontrendszer elemszáma is nagyobb ott.

Ez azt mutatja, hogy a bal homloklebeny kapcsolatai több mérték szerint is szignifikánsan gazdagabbak, mint a jobb homloklebenyéi. Hasonlóan az is kiderült, hogy a homloklebenyben ez a normált érték nagyobb, mint a fali lebenyben, és a fali lebenyben nagyobb, mint a halántéklebenyben.