Szélsőérték-számítási feladatok

Olvasási idő: 7 perc

1.) Bontsuk a 10-et két szám összegére úgy, hogy a két szám négyzetösszege minimális legyen!

MEGOLDÁS

10 = x + y

Célfüggvény: f(x) = x² + y² → minimális legyen

Mellékszámítások: y = 10 – x

Behelyettesítés: f(x) = x² + (10 – x)² = 2x² – 20x + 100

Deriválás: f'(x) = 4x – 20

f”(x) = 4

Minimum kiszámítása: 4x – 20 = 0 ⇒ x = 5 y = 5

elrejt

2.) Mekkorák az oldalai az 1 m kerületű (U), legnagyobb területű téglalapnak?

MEGOLDÁS

U = 1m = 2a + 2b

Célfüggvény: A(x) = a * b → maximális legyen

Mellékszámítások: 1 = 2(a + b)

$b = \frac{1}{2} - a$

Behelyettesítés:

$A(a) = a * (\frac{1}{2} - a) = \frac{1}{2}a - a^2$

Deriválás:

$A'(a) = \frac{1}{2} - 2a$

$A''(a) = -2$

Minimum kiszámítása:

$\frac{1}{2} - 2a = 0 \hspace{20}\Rightarrow a = \frac{1}{4}\hspace{20} (25 cm) \hspace{20} b = \frac{1}{4}$

Négyzet

elrejt

3.) Írjunk be egy legnagyobb területű téglalapot egy olyan háromszögbe, melynek c oldala 12 cm, magassága (h) 8 cm. A téglalap egyik oldala legyen a háromszög c oldalán.

MEGOLDÁS

$a = \frac{c}{2} \hspace{20}(6 cm)\hspace{20} b = \frac{h}{2} \hspace{20} (4 cm)$

elrejt

4.) Készítsünk egy V=1 dm³térfogatú négyzetes oszlop alakú kartont a legminimálisabb felszínnel!

MEGOLDÁS

V = 1 dm³ = 1000 cm³ = a² * b

Célfüggvény: V (a; b) = 2a² + 4ab → minimális legyen

Mellékszámítások: a² * b = 1000

$b = \frac{1000}{a^2}$

Behelyettesítés:

$V(a) = 2a^2 + 4a \frac{1000}{a^2} = 2a^2 + 4000 * a^{-1}$

Deriválás: V'(a) = 4a – 4000 * a^-2

V”(a) = 4a + 8000 * a^-3

Minimum kiszámítása: 4a – 4000 * a^-2 = 0 ⇒ a = 10 b = 10

Kocka

elrejt

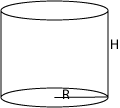
5.) Hogyan válasszuk meg a V=250p cm³térfogatú henger sugarát és magasságát, hogy a legminimálisabb felszínt kapjuk?

MEGOLDÁS

V = 250 * π cm³ = R² * π * H

R² * H = 250

Célfüggvény: A (R; H) = 2R² * π + 2RπH → minimális legyen

A (R; H) = 2R² + 2RH

Mellékszámítások:

$H = \frac{250}{R^2}$

Behelyettesítés:

$A(R) = 2R^2 + 2R * \frac{250}{R^2} = 2R^2 + \frac{500}{R}$

Deriválás: A'(R) = 4R – 500 * R^-2

A”(R) = 4 + 1000 * R^-3

Minimum kiszámítása: 4R – 500 * R^-2 = 0 ⇒ R = 5 H = 10

elrejt

6.) Az 5. feladat csak a henger legyen felül nyitott.

MEGOLDÁS

V = 250 * π cm³ = R² * π * H

R² * H = 250

Célfüggvény: A (R; H) = R² * π + 2RπH → minimális legyen

A (R; H) = R² + 2RH

Mellékszámítások:

$H = \frac{250}{R^2}$

Behelyettesítés:

$A(R) = 2R^2 + 2R * \frac{250}{R^2} = 2R^2 + \frac{500}{R}$

Deriválás: A'(R) = 2R – 500 * R^-2

A”(R) = 2 + 1000 * R^-3

Minimum kiszámítása: 2R – 500 * R^-2 = 0 ⇒

$R = 5 * \sqrt[3]{20}$

H = 1,35

elrejt

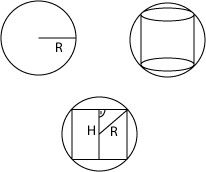
7.) Egy R=12 cm sugarú gömbbe írjunk:

a.) egy hengert a legnagyobb palástfelülettel

MEGOLDÁS

R = 12 cm

Célfüggvény: V (r; H) = 2rπH → maximális legyen

V (r; H) = 2rH

Mellékszámítások:

$H = \sqrt{576 - 4r^2}$

Behelyettesítés:

$V(r) = 2r * \sqrt{576 - 4r^2}$

Egyszerűsítés: V(r) = 4r² * (576 – 4r²) = 4r² * 576 – 16r⁴

Deriválás: V'(r) = 8 * 576r – 16 * 4r³

V”(r) = 8 * 576 – 192r²

Minimum kiszámítása: 8 * 576r – 16 * 4r³ = 0 ⇒ r = 8,5 H = 16,92

elrejt

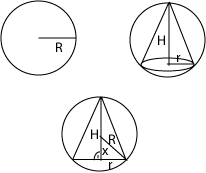
7.) Egy R=12 cm sugarú gömbbe írjunk:

b.) egy kúpot a legnagyobb térfogattal.

MEGOLDÁS

R = 12 cm

Célfüggvény:

$V (r; H) = \frac{r^2 \pi H}{3}$

→ maximális legyen

V (r; H) = r²H

Mellékszámítások: x² + r² = R²

H = R + x ⇒ x = H – R

$(H - R)^2 + r^2 = R^2 \Rightarrow r = \sqrt{2HR - H^2}$

Behelyettesítés:

$V(r; H) = ( \sqrt{2HR - H^2})^2 *H$

Egyszerűsítés: V(r; H) = (2HR – H²) * H = 24H² – H³

Deriválás: V'(r; H) = 48H * 3H²

V”(r; H) = 48 – 6H

Minimum kiszámítása: 48H – 3H² = 0 ⇒ r = 11,31 H = 16

elrejt

8.) Írjuk egy R=12 cm sugarú félgömbbe a legnagyobb térfogatú kúpot, melynek csúcsa a a félgömb középpontjában van.

MEGOLDÁS

R = 12 cm

Célfüggvény:

$V (r; H) = \frac{r^2 \pi H}{3}$

→ maximális legyen

V (r; H) = r²H

Mellékszámítások: H² + r² = R²

$H = \sqrt{144 - r^2}$

Behelyettesítés:

$V(r; H) = r^2 \sqrt{144 - r^2}$

Egyszerűsítés:

$V(r; H) = ( r^4 * (144 - r^2) = 144r^4 - r^6$

Deriválás: V'(r; H) = 576r³ – 6r⁵

V”(r; H) = 1728r² – 30r⁴

Minimum kiszámítása: 576r³ – 6r⁵ = 0 ⇒ r = 9,89 H = 6,84

elrejt

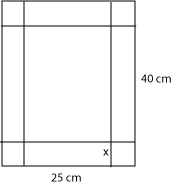
9.) Egy téglalap alakú lemezből, melynek oldalai l=40 cm és b=25 cm kell készítenünk egy téglatestet úgy, hogy a lemez sarkaiból egy négyzet alakú kis részt levágunk, és az így visszamaradt téglalapokat felhajtjuk. Mekkora legyen a négyzet oldala, hogy a legnagyobb térfogatú téglatestet kapjuk?

MEGOLDÁS

Célfüggvény: V(x) = G * H → maximális legyen

V(x) = (40 – 2x) * (25 – 2x) * x

V(x) = 4x³ – 130x² + 1000x

Deriválás: V'(x) = 12x² – 260x + 1000

V”(x) = -24x – 260

Minimum kiszámítása: 12x² – 260x + 1000 = 0

$\Rightarrow r_1 = 5 \hspace{20} r_2 = \frac{100}{6}$

elrejt

10.) Egy henger alakú üveg alján félgömböt helyeztünk el. A térfogata 45pi dm³. Mekkora legyen a henger sugara és a magassága, hogy az üveg a legkevesebb felülettel rendelkezzen?

MEGOLDÁS

V = 45π dm³

Célfüggvény: O (R; H) = R² + 2RH + 2R²→ minimális legyen

Mellékszámítások:

$V = R^2\pi H + \frac{4R^3 \pi}{3 *2} \Rightarrow R^2H + \frac{4R^3}{6} = 45$

$\Rightarrow H = \frac{270 - 4R^3}{6 R^2}$

Behelyettesítés:

$V = R^2 + 2R \frac{270 - 4R^3}{6R^2} + 4R^2 = 5R^2 + 90 R^{-1} - \frac {4}{3}R^2$

Deriválás:

$V' = 10R - 90R^{-2} - \frac{8}{3}R$

$V'' = 10 - \frac{8}{3} + 180R^{-3}$

Minimum kiszámítása:

$10R - 90R^{-2} - \frac{8}{3}R = 0 \hspace{20}\Rightarrow R = 2,3 \hspace{10}H = 6,9$

elrejt

7 hozzászólás

Gergő

2022/05/25
Válasz

6. Feladat
R=6,3 H=6,3
- TudományPláza
  
  2022/06/03
  Válasz
  
  ? Hogyan?
  - Kati
    
    2022/07/16
    Válasz
    
    6. feladat
    R=5 * \sqrt[3]{2}\], így R=6,3
Gergő

2022/05/25
Válasz

A 10.feladat célfüggvénye miszerint O (R; H) = R^2 + 2RH + 4R^2, itt a 4R^2 csak 2R^2 mivel egy félgömböt helyezünk rá.
Szabó-Pál Eszter

2020/04/09
Válasz

A 7. a) feladat megoldása R = M = 5 * \sqrt[3]{2}\]
- TudományPláza
  
  2020/04/24
  Válasz
  
  Kedves Eszter!
  R nem lehet egyenlö M-mel mert R eleve 12 cm volt a feladatban. (A gömb sugara)
  Átszámolva nekünk ugyanannyi jött ki, mint, ami a megoldásban van. De, ha megteszi, hogy levezeti azt megköszönjük.
  - Kis Anna
    
    2022/05/19
    Válasz
    
    Kár, hogy a 3. feladat nincs levezetve. 🙁