Maga a tétel a következőket mondja ki:

Az ABC derékszögű háromszög C csúcsánál derékszög van, ha a C pont az AB szakasz mint átmérő fölé írt félkörön van, kivéve az A és B pontokat.

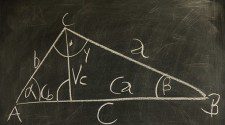
A Thalész-tétel bizonyítása

A tétel bizonyításához az O középpontú kör átmérőjére rajzolt megfelelő ABC háromszög A-nál lévő szögét α-val, a B-nél levő szögét β-val jelöljük.

OC sugár meghúzásával egy AOC és BOC egyenlő szárú háromszögeket kapunk, ami a fenti ábrán is látható. Ezek alapján a belső szögek összege a következőképpen alakul:

α + β + (α + β) = 180°,

α + β = 90°.

Látható, hogy az ABC háromszög valóban derékszögű.