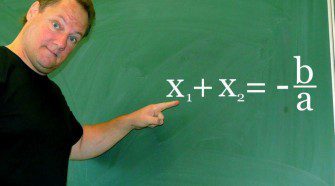
Szöveges feladatok megoldása elsőfokú egyenletekkel kezdőknek 1.
A bonyolult szöveges feladatok megoldása sokak számára jelent problémát, azonban szeretnénk megmutatni, hogy egy egyszerű logikát követve a megoldás elsőfokú egyenletekkel nem is olyan bonyolult. Egy korábbi cikkünkben már bemutattuk, hogyan kell számolni algebrai kifejezésekkel, ezért most szeretnénk bemutatni, hogy az egyszerű szöveges feladatok megoldása elsőfokú egyenletekkel is lehetséges. Az egyenlet definíciója: bármely két egyenlőségjellel …

Diszkrimináns
ha D > 0, két megoldása van az egyenletnek, ha D = 0, egy megoldása van az egyenletnek, ha D < 0, egy valós megoldása sincs az egyenletnek. Megtekintés: 252

Harmadfokú egyenletek
A harmadfokú egyenlet általános megoldóképlete nagyon bonyolult, és emellett gyakorlatban is alig használják. De egynéhány esetben egy harmadfokú egyenletet vissza tudunk vezetni egy másodfokúra.

Horner-elrendezés
A Horner-elrendezés (William George Horner, 1786-1837) segítségével ki tudjuk a polinom értéket számolni, és egyúttal el tudjuk osztani a polinomot egy lineáris faktorral.

Negyedfokú egyenletek
Niels Henrik Abel bizonyította be 1824-ben, hogy a negyedfokú egyenlet a legmagasabb fokú egyenlet, amely általános alakban megoldható.
Többismeretlenes egyenletek
Szorzathalmaz A szorzathalmaz A×B (ejtsd „A kereszt B”) két halmaz A és B rendezett számpárjaiból áll, amiknek az első eleme az A halmazból a második eleme pedig a B halmazból való. A × B = {(x ; y) ¦ (x e A) és (y e B)} Példa: A = {1; 2; 3} B={1; 2} A × …

Kétismeretlenes elsőfokú egyenlet
Az egyenletrendszer bármely egyenletét külön-külön végtelen sok számpár elégíti ki. A számpárokat egy-egy egyenessel szemléltethetjük a koordináta-rendszerben.

Többismeretlenes lineáris egyenletrendszer
A megoldáshalmaz a következő alakú egyenletnél ax + by + cz = d végtelen sok számhármasból áll. A megfelelő pontok a tér (R³) egy síkján helyezkednek el. Egy háromismeretlenes egyenletrendszer (3 egyenlet) megoldásai három sík metszete. A megoldáshalmaz állhat egy pontból, vagy egy egyenesből, vagy akár egy síkból. Vagy lehet akár teljesen üres is. Néhány …