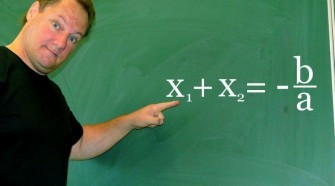Szöveges feladat megoldása egyenlettel kezdőknek 3
Az előző héten már bemutattuk, hogy a szöveges feladat megoldása egyenlettel, kezdők számára sem bonyolult feladat. Most itt egy újabb „szöveges feladat megoldása egyenlettel kezdőknek” bejegyzéssel készültünk, amelyben a feladat az előzőeknél már egy kicsivel összetettebb. Három lány (Anita, Betti és Cecília) aggódott a súlyáért, ezért mérlegre állt. Ez életszerű feladat! Amikor Anita és Betti …

Szöveges feladatok megoldása elsőfokú egyenletekkel kezdőknek 2.
A szöveges feladatok megoldása bárkinek jelenthet problémát, de most megmutatjuk, hogy nem olyan nehéz, mint amilyennek látszik. Az előző cikkünkben már bemutattuk, hogy szöveges feladatok megoldása elsőfokú egyenletekkel egy egyszerű szöveges feladat esetében nem is olyan bonyolult. Most második feladatként nézzük az előző egy picit összetettebb változatát! Egy csomag rágógumi és egy tábla csoki összesen …
Szöveges feladatok megoldása elsőfokú egyenletekkel kezdőknek 1.
A bonyolult szöveges feladatok megoldása sokak számára jelent problémát, azonban szeretnénk megmutatni, hogy egy egyszerű logikát követve a megoldás elsőfokú egyenletekkel nem is olyan bonyolult. Egy korábbi cikkünkben már bemutattuk, hogyan kell számolni algebrai kifejezésekkel, ezért most szeretnénk bemutatni, hogy az egyszerű szöveges feladatok megoldása elsőfokú egyenletekkel is lehetséges. Az egyenlet definíciója: bármely két egyenlőségjellel …
Egyismeretlenes egyenletek
Az A(x) = B(x) kifejezést egyenletnek nevezzük, ahol x az ismeretlen. A és B tetszőleges algebrai kifejezések. (Az ismeretlent természetesen jelölhetjük más betűvel is!) Alaphalmaz: minden olyan szám, ami az egyenletbe behelyettesíthetőnek tűnik. (jelölése: A) Definícióhalmaz: minden elem az alaphalmazból, amelyet az egyenletbe helyettesíthetünk. (jelölése: D) Megoldáshalmaz: minden elem a definícióhalmazból, amelyet az egyenletbe helyettesítve …

Ekvivalens átalakítások
Egy egyenlet megoldáshalmaza nem változik, ha mindkét oldalát a következőképpen változtatjuk: ugyanazt a számot (kifejezést) adjuk, illetve vonjuk ki mindkét oldalból ugyanazzal a számmal (kifejezéssel) (szám, illetve kifejezés nem lehet nulla) megszorozzuk mindkét oldalt ugyanazzal a számmal (kifejezéssel) (szám, illetve kifejezés nem lehet nulla) osztjuk mindkét oldalt. Mindig megpróbálunk egy egyenletet ekvivalens átalakításokkal a lehető …

Diszkrimináns
ha D > 0, két megoldása van az egyenletnek, ha D = 0, egy megoldása van az egyenletnek, ha D < 0, egy valós megoldása sincs az egyenletnek. Megtekintés: 227

Harmadfokú egyenletek
A harmadfokú egyenlet általános megoldóképlete nagyon bonyolult, és emellett gyakorlatban is alig használják. De egynéhány esetben egy harmadfokú egyenletet vissza tudunk vezetni egy másodfokúra.