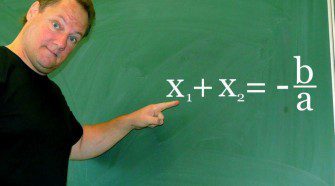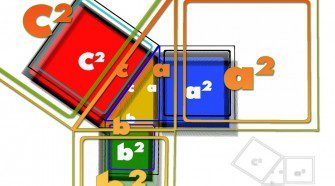
Pythagoras tétele
Minden derékszögű háromszögben a befogók négyzetösszege egyenlő az átfogó négyzetével. Bizonyítás: 1. Terület c2 = a2 + b2 2. Szög α + β + γ = 180 ° γ = 90 ° Megtekintés: 440
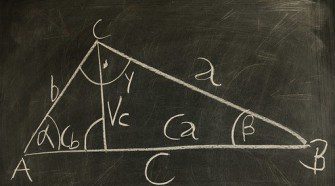
Magasságtétel és befogótétel
Magasságtétel Minden derékszögű háromszögben az átfogó magasságának a talppontja az átfogót két olyan részre bontja, melyeknek a magasság a mértani közepe. h2 = pq Befogótétel Minden derékszögű háromszögnek egy befogója mértani közepe az átfogónak és a befogó átfogóra eső vetületének. a2 = cq b2 = cp Megtekintés: 8 274

Ekvivalens átalakítások
Egy egyenlet megoldáshalmaza nem változik, ha mindkét oldalát a következőképpen változtatjuk: ugyanazt a számot (kifejezést) adjuk, illetve vonjuk ki mindkét oldalból ugyanazzal a számmal (kifejezéssel) (szám, illetve kifejezés nem lehet nulla) megszorozzuk mindkét oldalt ugyanazzal a számmal (kifejezéssel) (szám, illetve kifejezés nem lehet nulla) osztjuk mindkét oldalt. Mindig megpróbálunk egy egyenletet ekvivalens átalakításokkal a lehető …

Diszkrimináns
ha D > 0, két megoldása van az egyenletnek, ha D = 0, egy megoldása van az egyenletnek, ha D < 0, egy valós megoldása sincs az egyenletnek. Megtekintés: 252

Harmadfokú egyenletek
A harmadfokú egyenlet általános megoldóképlete nagyon bonyolult, és emellett gyakorlatban is alig használják. De egynéhány esetben egy harmadfokú egyenletet vissza tudunk vezetni egy másodfokúra.

Horner-elrendezés
A Horner-elrendezés (William George Horner, 1786-1837) segítségével ki tudjuk a polinom értéket számolni, és egyúttal el tudjuk osztani a polinomot egy lineáris faktorral.

Negyedfokú egyenletek
Niels Henrik Abel bizonyította be 1824-ben, hogy a negyedfokú egyenlet a legmagasabb fokú egyenlet, amely általános alakban megoldható.