Medve Matek Élménynap
Sokan, sok mindent megtesznek azért, hogy a lehető legizgalmasabb élménnyé varázsolják a matematikát. A Matematika Összeköt Egyesület tagjai elhivatott fiatal matematikusok, fizikusok és egyetemi hallgatók, akiknek szívügye a tehetséggondozás és az élményalapú matematikaoktatás népszerűsítése. A többféle program között az egyik a Medve Matek Élménynap. Ez egy ingyenes nyílt nap, ahol tanárok, diákok és szülők is …
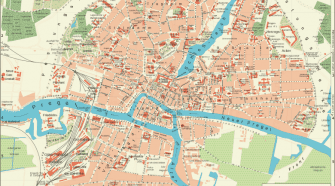
Euler königsbergi hídjai
Königsberg – a mai Kalinyingrád – Leonhard Euler svájci matematikus révén vonult be a tudománytörténelembe. A város hét hídjának elhelyezkedéséből származtatott, euleri gondolatkísérlet szolgált az első gráfelméleti probléma alapjául. Königsberg, régi és gazdag történelmű városa a Pregel folyó két partján fekszik. Euler korában, a XVIII. század első harmadában a várost, valamint két szigetét, hét híd …
Zárójelek felbontása bonyodalom nélkül
A matematikai képletekben a jó megoldás érdekében alkalmazkodni kell a matematikai műveletek sorrendiségének szabályához. Tehát csak abban az esetben haladhatunk a számolással folyamatosan balról jobbra, ha egy műveletsorban kizárólag összeadás és kivonás, vagy kizárólag szorzás és osztás van. Ha egy műveletsorban vegyesen vannak az alapműveletek, akkor először a szorzásokat és osztásokat, majd az összevonásokat és …
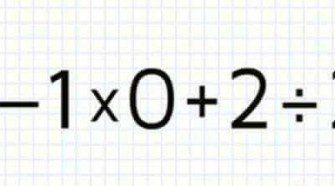
Vicces matematika
Senki nem mondhatja, hogy a matematika nem vicces, vagy hogy a matematika nem alkalmas viccelődésre. A humor igenis a matematika szerves része tud lenni. Éppen ezért összegyűjtöttünk néhány viccet, amitől biztosan gurulni fogsz a nevetéstől. Ez a vicces matematika: 1. Egy mérnök, egy fizikus és egy matematikus azt a feladatot kapja, hogy mérje meg egy …
Meghalt Császár Ákos matematikus
Életének 94. évében meghalt Császár Ákos matematikus, egyetemi tanár, a Magyar Tudományos Akadémia rendes tagja csütörtökön. A Kossuth-díjas matematikus tudományos tevékenységének két fő területe a valós függvénytan és a topológia volt. Az 1940-es, 1950-es években írt valós függvénytani munkái kiemelkedő, ma már klasszikusnak számító eredményeket tartalmaznak. Az 1950-es évek végétől érdeklődése a topológia felé fordult, majd az …
Humoros matematika
Következő összeállításunk egy olyan gyűjtés, amely a matematika mindennapjaiban találja meg a humort. Vizsgaidőszakban Tanárok és vizsgázók eltérő véleménye ugyanarról az eseményről. Párhuzamok (T) := Tanárok egymás közötti beszélgetéséből. (V) := Vizsgázók egymás közötti beszélgetéséből, a folyosón, nyomban a vizsga után. (T) Összezavarodott nálam az egyik vizsgázó, de elnéző voltam vele. Úgy tettem, mintha nem …
Vicces matematika
– Jean! – Igen, uram! – Kérek egy 9 perces főtt tojást! – De uram! Nekünk csak 4 perces és 7 perces homokóránk van! – Ez engem nem érdekel! Én más tojást nem eszem! Mit tegyen Jean, hogy eleget tegyen urának? Megoldás: A homokórák „állását” a következőképpen jelölném: például a 7 perces homokórában 4 …
Könyvajánló – a matematika szeretetéért
Kjartan Poskitt: Agyatlan algebra Először megtanultál tízig összeadni. Micsoda izgalom! Aztán a fejedbe verték az egyszeregyet. Te jó ég! Most pedig a kezedbe nyomják az Agyatlan algebrát. Ami mulatságos, érdekes, sőt mi több, a gyilkos egyenletek és unalmas összegek is kimaradtak belőle! Róka Sándor: Humor a matematikában A könyvben található történetek bemutatják a matematika, …
Feladatok függvényvizsgálathoz
Vizsgáld meg és rajzold fel a következő függvények képét! (Zérushelyek, szélsőértékek, inflexiós pont, az inflexiós pontba húzott érintő egyenlete.) 1.) f(x) = x2 – x – 2 2.) f(x) = x3 – 6×2 + 9 3.) 4.) 5.) 6.) f(x) = x3 – 3×2 + 4 …
Megoldási séma szélsőértékfeladathoz
A gyakorlatban gyakran állunk szemben olyan feladattal, hogy egy mennyiséget (terület, felszín, térfogat, anyagfelhasználás, költség stb.) optimalizálnunk kell.
Ha a mennyiséget egy egyváltozós függvénnyel kifejezhetjük, akkor az 1. derivált segítségével kiszámíthatjuk a szélsőértéket. Ha több változó fordul elő, akkor ezeket először ki kell fejezni egy változó segítségével.
