
Megoldási séma szélsőértékfeladathoz
A gyakorlatban gyakran állunk szemben olyan feladattal, hogy egy mennyiséget (terület, felszín, térfogat, anyagfelhasználás, költség stb.) optimalizálnunk kell.
Ha a mennyiséget egy egyváltozós függvénnyel kifejezhetjük, akkor az 1. derivált segítségével kiszámíthatjuk a szélsőértéket. Ha több változó fordul elő, akkor ezeket először ki kell fejezni egy változó segítségével.

Szélsőérték-számítási feladatok
1.) Bontsuk a 10-et két szám összegére úgy, hogy a két szám négyzetösszege minimális legyen! 2.) Mekkorák az oldalai az 1 m kerületű (U), legnagyobb területű téglalapnak? 3.) Írjunk be egy legnagyobb területű téglalapot egy olyan háromszögbe, melynek c oldala 12 cm, magassága (h) 8 cm. A téglalap egyik oldala legyen a háromszög …
Feladatok és megoldások deriválás témakörben
1.) Számítsd ki a következő függvények deriváltjait! a.) f(x) = x100 b.) f(x) = 3×5 c.) f(x) = 5×12 d.) f(x) = 0,5×4 e.) f.) f(x) = 3×3 + 4×2 – 5x g.) f(x) = x4 – 6×3 + 5×2 + 3 h.) f(x) = 2×3 – 12×2 + 7x – …

A differenciálhányados
Probléma Keressük az f függvény változását az x helyen. Geometriai szemléltetés Az érintő meredeksége a P(x ; f(x)) pontban: A P, Q pontokon átmenő szelő (zöld vonal) meredeksége: Ezt a kifejezést nevezzük DIFFERENCIAHÁNYADOSNAK. Minél jobban közeledik a Q pont a P ponthoz, annál meredekebb a szelő. Mikor P és Q egybeesik, a …

A háromszögek fajtái
A háromszög egy olyan sokszög, melynek három oldala van. A három oldalból következően pedig három csúcsa is van. A csúcsokat nagybetűvel (A, B, C) szokták jelölni.
A háromszög oldalait kisbetűvel (a,b,c) jelöljük. Az erre vonatkozó szabály szerint úgy, hogy az A csúccsal szemközti oldalt a-val, a B csúccsal szemközti oldalt b-vel, a C csúccsal szemközti oldalt pedig c-vel.
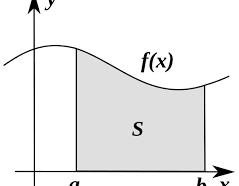
Primitív függvények (Határozatlan integrál)
Az analízis legfontosabb részterülete az integrálszámítás. Ha a primitív függvényeket vizsgáljuk rögtön egy definícióval kezdhetjük.

Fontosabb függvények primitív függvényei
A legfontosabb elemi függvények primitív függvényei levezethetőek, de mi ezt kihagyjuk. Megtekintés: 1 253

A 2. derivált jelentése
A 2. derivált jelentése – A 2. derivált a meredekség változását adja meg. Tehát információt tudhatunk meg a függvény görbületeiről.

Fordított feladatok függvényvizsgálathoz
Ezeknél a feladatoknál a függvény egyenletét kell megkeresni néhány megadott pont alapján. Írjuk először fel a függvények általános egyenletét! Például Harmadfokú polinomfüggvény: f(x) = ax3 + bx2 + cx + d Negyedfokú polinomfüggvény: f(x) = ax4 + bx2 + c (ez szimmetrikus az y tengelyre nézve!) (A szimmetria miatt a páratlan kitevők elhagyhatóak.) Ezekből képezzük …
A függvény nevezetes pontjai
Összefoglalva: Metszéspontok az y-tengellyel x = 0 Zérushelyek (metszéspontok az x-tengellyel) f(x) = 0 (y =0) Szélsőértékhelyek f'(x) = 0 A megtalált értéket behelyettesítve 2. deriváltba: f”(x) < 0: maximum f”(x) > 0: minimum Inflexiós pontok f”(x) = 0; f”'(x) ≠ 0 Az inflexiós pontba húzott érintőt megkapjuk, ha a kapott értéket behelyettesítjük az 1. deriváltba. Megtekintés: 482


