Feladatok az alapfogalmakhoz
1. Írd fel a következő összefüggéseket függvényként!
| a.) Benzinár: 1,2 €/l x: ismert liter, p(x): ár |
MEGOLDÁS
elrejt |
| b.) Telefonszámla: alapköltség: ATS 26 € kapcsolási díj: 9,30 € tarifaegységenként x: tarifaegységek száma R(x): számladíj |
MEGOLDÁS
elrejt |
| c.) Taxiutazás: alapdíj: ATS 28 € kilométerár: ATS 8 € x: megtett kilométer, F(x): ár |
MEGOLDÁS
elrejt |
| d.) Egy olajtank 500 l olajat képes tárolni. Napi felhasznált mennyiség: 35 l t: idő napokban, R(t): megmaradt olajmennyiség |
MEGOLDÁS
elrejt |
2.) A következő függvények adottak, értelmezési tartományuk az ![]() !
!
f1 : x → x + 1
f2 : x → 2x
f3 : x → x2
f4 : x → ![]()
| a.) Rajzold meg a függvények képét értéktáblázat segítségével a [-3; 3] intervallumban! Ügyelj az értelmezési tartományokra!) |
|
f1 : x → x + 1 MEGOLDÁS
elrejt MEGOLDÁS
elrejt MEGOLDÁS
elrejt MEGOLDÁS a 0 x érték nem megengedett az osztás miatt elrejt |
| b.) Add meg az adott függvények inverzfüggvényét, ha létezik! Példa: f : x = x – 2 → f-1 : x = y – 2 ⇒ y = x + 2 |
MEGOLDÁS
elrejt |
|
c.) Add össze az adott függvényeket! |
| c/1.) f1 + f3 | MEGOLDÁS f1 + f3 ⇒ x2 + x + 1 elrejt |
| c/2.) f2 + f3 | MEGOLDÁS f2 + f3 ⇒ x2 + 2x elrejt |
| c/3.) f2 + f4 | MEGOLDÁS
elrejt |
| c/4.) f3 + f4 | MEGOLDÁS
elrejt |
| d.) Szorozd össze az adott függvényeket! Példa: f1(x) . f2(x) = (x + 1) . 2x = 2x2 + 2x |
|
| d/1.) f1 . f3 | MEGOLDÁS
elrejt |
| d/2.) f2 . f3 | MEGOLDÁS
elrejt |
| d/3.) f2 . f4 | MEGOLDÁS
elrejt |
| d/4.) f3 . f4 | MEGOLDÁS
elrejt |
| e.) Add meg a következő összetett függvényeket! Példa: f1(f2(x)) =2x + 1, de f2(f1(x)) = 2(x+1) = 2x + 2 |
|
| e/1.) f1(f3(x)) | MEGOLDÁS f1(f3(x)) ⇒ x2 + 1 elrejt |
| e/2.) f3(f1(x)) | MEGOLDÁS f3(f1(x)) ⇒ (x + 1)2 elrejt |
| e/3.) f1(f4(x)) | MEGOLDÁS
elrejt |
| e/4.) f4(f1(x)) | MEGOLDÁS
elrejt |
| e/5.) f2(f3(x)) | MEGOLDÁS
elrejt |
| e/6.) f3(f2(x)) | MEGOLDÁS
elrejt |
| e/7.) f2(f4(x)) | MEGOLDÁS
elrejt |
| e/8.) f4(f2(x)) | MEGOLDÁS
elrejt |
Feladatok a lineáris függvényekhez
| 1.) Számold ki a zérushelyeket, a fixértéket és add meg az inverzfüggvényeket a következő függvényeknél! (Zérushely: f(x) = 0, fixérték: f(x) = x) Rajzold meg a függvényt! |
|
| a.) f : y = 2x – 3 | |
|
MEGOLDÁS Zérushely:
Fixérték: Inverzfüggvény:
elrejt |
|
| b.) f : y = -3x + 6 | |
MEGOLDÁS Zérushely:
Fixérték: Inverzfüggvény:
elrejt |
|
| c.) f : y = |
|
MEGOLDÁS Zérushely:
Fixérték: Inverzfüggvény:
elrejt |
|
| d.) f : y = |
|
MEGOLDÁS Zérushely:
Fixérték: Inverzfüggvény:
elrejt |
|
| e.) f : y = x – 5 | |
MEGOLDÁS Zérushely:
Fixérték: Inverzfüggvény:
elrejt |
|
| f.) f : y = |
|
MEGOLDÁS Zérushely:
Fixérték: Inverzfüggvény:
elrejt |
|
| g.) f : y = -0,5x – 3 | |
MEGOLDÁS Zérushely:
Fixérték: Inverzfüggvény:
elrejt |
|
| h.) f : y = 7 – x | |
MEGOLDÁS Zérushely:
Fixérték: Inverzfüggvény:
elrejt |
|
| 2.) Add meg a lineáris függvény egyenletét, mely átmegy az origón és a megadott P ponton! | |
| a.) P (4; 6) | MEGOLDÁS
elrejt |
| b.) P (12; 3) | MEGOLDÁS
elrejt |
| c.) P (-3; 9) | MEGOLDÁS
elrejt |
| d.) P (8; -5) | MEGOLDÁS
elrejt |
| e.) P (-1; -7) | MEGOLDÁS
elrejt |
| f.) P (2,5; -7,5) | MEGOLDÁS
elrejt |
| 3.) Add meg a lineáris függvény egyenletét, mely átmegy a megadott P ponton és a meredeksége k: | |
| a.) P (4; 6) k = 1 | MEGOLDÁS
elrejt |
| b.) P (3; 1) k = 2 | MEGOLDÁS
elrejt |
| c.) P (4; 4) k = |
MEGOLDÁS
elrejt |
| d.) P (-3; -5) k = |
MEGOLDÁS
elrejt |
| e.) P (4; -2) k = -3 | MEGOLDÁS
elrejt |
| f.) P (6; 0) k = |
MEGOLDÁS
elrejt |
| 4.) Add meg a lineáris függvény egyenletét, amely átmegy az A és B pontokon! |
| a.) A (4; 6), B (3; 5) | MEGOLDÁS
elrejt |
| b.) A (-2; 4), B (2; 2) | MEGOLDÁS
elrejt |
| c.) A (-3; 2), B (6; 8) | MEGOLDÁS
elrejt |
| d.) A (-1; -1,5), B (3; -7,5) | MEGOLDÁS
elrejt |
| e.) A (1; 2), B (-1; -3) | MEGOLDÁS
elrejt |
| f.) A (3; 1,8), B (8; 2,3) | MEGOLDÁS
elrejt |
| 5.) Oldd meg a következő egyenletrendszereket grafikusan! | |
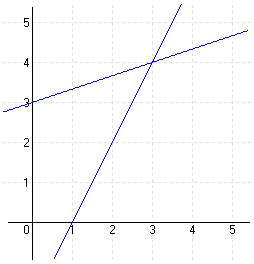
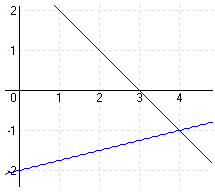
| a.) I. 2x – y = 2 II. -x + 3y = 9 |
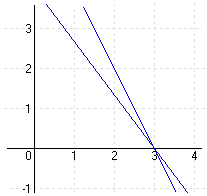
b.) I. 3x + y = -3 II. 3x + 4y = 6 |
MEGOLDÁS
elrejt |
MEGOLDÁS elrejt |
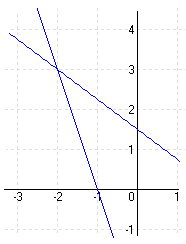
| c.) I. 2x + y = 6 II. 4x + 3y = 12 |
d.) I. x – 4y = 8 II. x + y = 3 |
MEGOLDÁS
elrejt |
MEGOLDÁS
elrejt |
| 6.) Egy mobiltelefon-társaság a következő tarifákat kínálja: Értékkártya: 0,60 €/perc Tarifa A: 0,20 €/perc, 10 € alapdíj Tarifa B: 0,10 €/perc, 20 € alapdíj |
|
| a.) Add meg a számlát a lebeszélt idő függvényeként minden tarifánál! | |
MEGOLDÁS 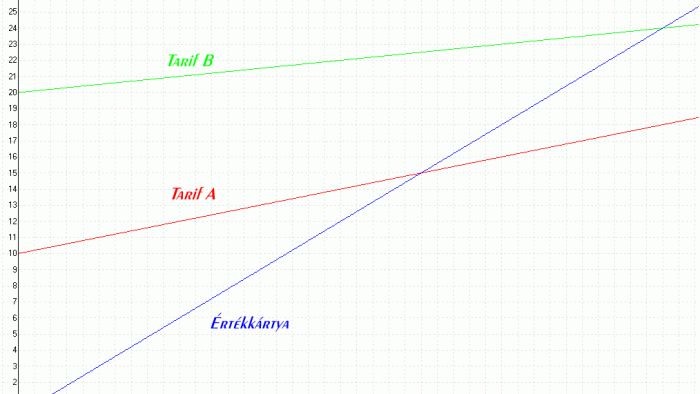 elrejt |
|
| b.) Mennyi az egyes tarifáknál a számladíj, ha 1 órát beszélünk egy hónapban? | MEGOLDÁS Értékkártya: w(x) = 0,6x 1 óra = 60 perc w(x) = 0,6 * 60 = 36 €
elrejt |
| c.) Hányadik perctől lesz a tarifa A olcsóbb, mint az értékkártya? | MEGOLDÁS 0,6x > 0,2x + 10
elrejt |
| d.) Hányadik perctől lesz a tarifa B olcsóbb, mint a tarifa A? | MEGOLDÁS 0,2x + 10 > 0,1x + 20
elrejt |
| e.) Ábrázold a 3 függvényt egy koordináta rendszerben! 20 perc = 1 cm, 10 € = 1 cm | |
| 7. ) Egy taxiút 2,50 € alapdíjba és 0,96 €-ba kerül kilométerenként: | |
| a.) Ábrázold az utazási költséget F(x) a megtett út x függvényében! | |
MEGOLDÁS 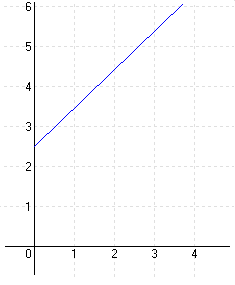 elrejt |
|
| b.) Mennyibe kerül egy 6 km-es út? | |
MEGOLDÁS F(x) = 0,96x + 2,50
elrejt |
|
| c.) Milyen messze jutunk 10 €-val? | |
MEGOLDÁS 0,96x + 2,5 = 10
elrejt |
|
Feladatok a másodfokú függvényekhez
| 1.) Ábrázold a következő függvényeket értéktáblázat segítségével a megadott intervallumban és számold ki a zérushelyeket! | |||||||||||||
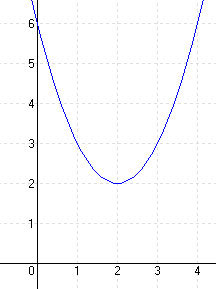
| a.) f(x) = x2 – 2 [-2; 2] | |||||||||||||
|
MEGOLDÁS Zérushely:
elrejt MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS 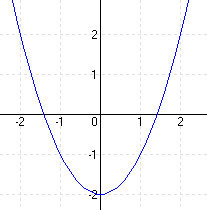 elrejt |
|||||||||||||
| b.) f(x) = x2 – 4x [-1; 5] | |||||||||||||
|
MEGOLDÁS
elrejt MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS 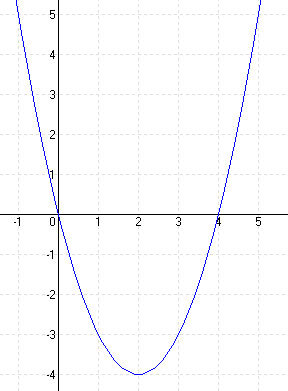 elrejt |
|||||||||||||
| c.) f(x) = 2x2 – 2x – 4 [-2; 3] | |||||||||||||
|
MEGOLDÁS
elrejt MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS 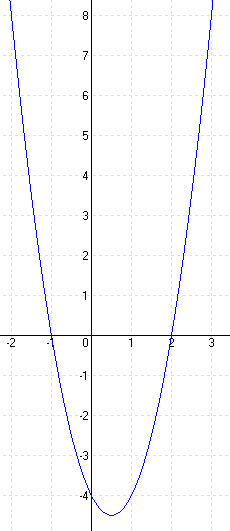 elrejt |
|||||||||||||
| d.)
[-5; 1] |
|||||||||||||
|
MEGOLDÁS
elrejt MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS 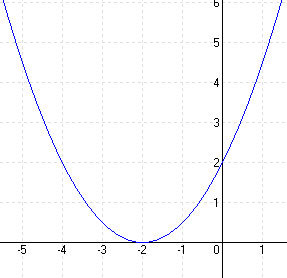 elrejt |
|||||||||||||
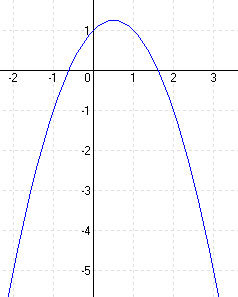
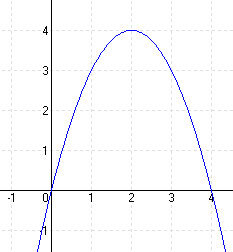
| e.) f(x) = -x2 + x + 1 [-2; 3] | |||||||||||||
|
MEGOLDÁS Zérushely:
elrejt MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS elrejt |
|||||||||||||
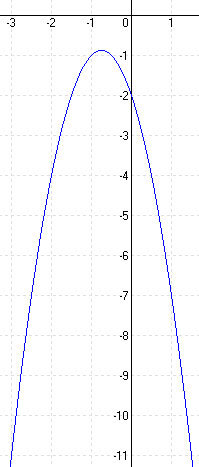
| f.) f(x) = -2x2 – 3x – 2 [-3; 1] | |||||||||||||
|
MEGOLDÁS Zérushely:
elrejt
|
| 2.) Számold ki a következő parabolák tengelypontját és metszéspontjait az x tengellyel, majd ábrázold őket! |
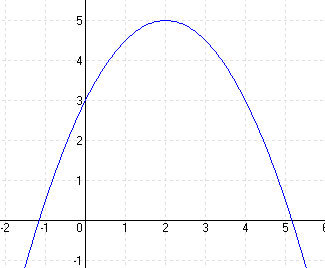
| a.) y = x2 – 6x + 11 |
MEGOLDÁS y = x2 – 6x + 11 = (x – 3)2 – 9 + 11 = (x – 3)2 + 2 ⇒ T (3; 2) (x – 3)2 + 2 = 0 ⇒ (x – 3)2 = -2 ⇒ nincs zérushely
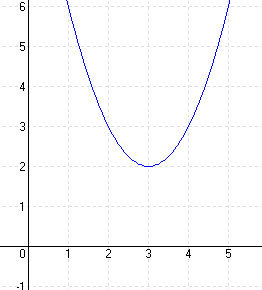 elrejt |
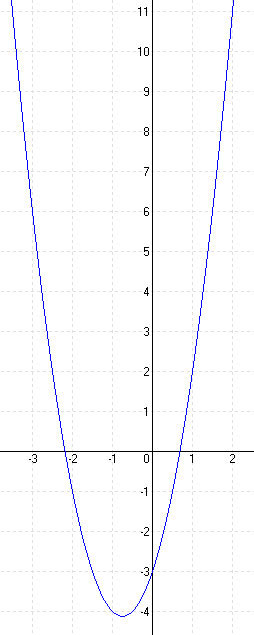
| b.) y = x2 – 2x – 3 |
MEGOLDÁS y = x2 – 2x – 3 = (x – 1)2 – 1 – 3 = (x – 3)2 – 4 ⇒ T (1; -4) (x – 1)2 – 4 = 0 ⇒ (x – 1)2 = 4 ⇒ x1 = 3 és x2 = -1
 elrejt |
| c.) y = x2 + 4x + 3 |
MEGOLDÁS y = x2 + 4x + 3 = (x + 2)2 – 4 + 3 = (x + 2)2 – 1 ⇒ T (-2; -1) (x + 2)2 – 1 = 0 ⇒ (x + 2)2 = 1 ⇒ x1 = -1 és x2 = -3
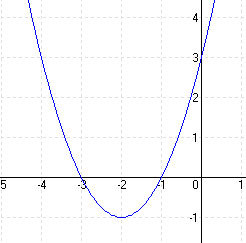 elrejt |
| d.) y = x2 + 5x + 7 |
MEGOLDÁS y = x2 + 5x + 7 = (x + 2,5)2 – 6,25 + 7 = (x + 2,5)2 + 0,75 ⇒ T (-2,5; -7,5) (x + 2,5)2 + 0,75 = 0 ⇒ (x + 2,5)2 = -0,75 ⇒ nincs zérushely
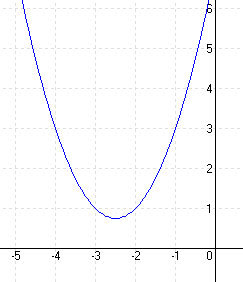 elrejt |
|
3.) Számold ki a másodfokú függvények egyenletét, melynek grafikonja átmegy a megadott pontokon! Ábrázold a függvényt és számítsd ki a zérushelyeket! Példa: A (0; 2) B (1; 1) C (3; 5) f : y = ax2 + bx + c A ∈ f : 2 = a . 02 + b . 0 + c |
|
| a.) A (0; 6) B (1; 3) C (2; 2) |
MEGOLDÁS f : y = ax2 + bx + c
A ∈ f : 6 = a . 02 + b . 0 + c ⇒ c = 6 elrejt |
| b.) A (0; 0) B (2; 4) C (3; 3) |
MEGOLDÁS f : y = ax2 + bx + c
A ∈ f : 0 = a . 02 + b . 0 + c ⇒ c = 0 elrejt |
| c.) A (-1; -4) B (1; 2) C (2; 11) |
MEGOLDÁS f : y = ax2 + bx + c
A ∈ f : -4 = a . -12 + b . -1 + c ⇒ -4 = a – b + c Zérushelyek: elrejt |
| d.) A (1; 4,5) B (2; 5) C (4; 3) |
MEGOLDÁS f : y = ax2 + bx + c
A ∈ f : 4,5 = a . -12 + b . -1 + c ⇒ 4,5 = a + b + c ⇒ c = 4,5 – a – b
Zérushelyek:
elrejt |







No Comment