Feladatok

Feladatok integrálszámítás

27.4k Views
Feladatok integrálszámítás
Olvasási idő: 8 perc

1.) Számítsd ki a következő függvények primitív függvényeit!

a.)  f(x) = 3x

MEGOLDÁS

    \[\int {3x} \hspace{2}{dx} = 3\int {x}\hspace{2} {dx} = 3 \frac{x^2}{2} + C\]

 

elrejt

 
b.)  f(x) = 8x3

MEGOLDÁS

 

    \[\int {8x^3} \hspace{2} dx = 8\int {x^3}\hspace{2} {dx} = 8 \frac{x^4}{4} + C = 2x^4 + C\]

 

elrejt

 
c.)  f(x) = x2 + x

MEGOLDÁS

 

    \[\int {x^2} + x \hspace{2} dx = \int {x^2}\hspace{2} {dx} + \int {x} \hspace{2} {dx}= \frac{x^3}{3} + \frac{x^2}{2} + C \]

 

elrejt

 

d.) f(x) = 3x2 + 4x + 1

MEGOLDÁS

 

    \[\int {3x^2} +4x + 1\hspace{1} dx =\int {3x^2}\hspace{1}{dx} + \int {4x} \hspace{1}{dx}+ \int {1 dx}= \]

    \[\ = x^3 + 2x^2 + x + C\]

elrejt

e.) f(x) = x6 – 3x5 + 7x3 

MEGOLDÁS

 

    \[\int {x^6} - 3x^5 + 7x^3 \hspace{2} dx = \int {x^6}\hspace{2} {dx} - \int {3x^5} \hspace{2} {dx} + \int {7x^3\hspace{2} {dx} = \]

 

    \[ = \frac{x^7}{7} - \frac{x^6}{2} + 7 \frac{x^4}{4} + C\]

elrejt
f.) 

    \[f(x) = \frac{x^2}{3} + \frac{x}{4}\]

MEGOLDÁS

 

    \[\int {\frac {x^2}{3} + \frac{x}{4}} \hspace{2} dx = \int {\frac {x^2}{3}\hspace{2} {dx} + \int {\frac {x}{4} \hspace{2} {dx}= \frac{x^3}{9} + \frac{x^2}{8} + C \]

 

elrejt

 
g.) 

    \[f(x) = \frac {x^4}{10} - 3x^2 + \frac{2}{3}\]

 

MEGOLDÁS

 

    \[\int {\frac {x^4}{10} - 3x^2 + \frac{2}{3}} \hspace{2} dx = \frac{x^5}{50} - x^3 + \frac{2x}{3} + C \]

 

elrejt

 
h.) 

    \[f(x) = \frac {1}{x^2}\]

 

MEGOLDÁS

 

    \[\int {\frac {1}{x^2} \hspace{2} dx = \int {x^{-2}} \hspace{2} {dx}= -\frac {1}{x} + C \]

 

elrejt

 
i.)

    \[f(x) = \frac {1}{x^3}\]

 

MEGOLDÁS

 

    \[\int {\frac {1}{x^3} \hspace{2} dx = \int {x^{-3}} \hspace{2} {dx}= -\frac {1}{2x^2} + C \]

 

elrejt
j.)

    \[f(x) = \sqrt {x}\]

 

MEGOLDÁS

 

    \[\int {\sqrt {x} \hspace{2} dx = \int {x^{\frac{1}{2}} \hspace{2} {dx}= \frac {2}{3} x^{\frac{3}{2}} + C \]

 

elrejt

 

2.) Add meg a következő függvények egyenletét, ha azok deriváltjai és egy pontjuk adott!

a.) f'(x) = 4x           P (2; 5)

MEGOLDÁS

 

    \[\int 4x \hspace{2}dx = 2x^2 + C \]

2 . 22 + C = 5   ⇒ 8 + C = 5    ⇒ C = -3 

F(x) = 2x2 – 3

elrejt
b.) f'(x) = 2x – 3           P (1; 0)

MEGOLDÁS

 

    \[\int 2x - 3 \hspace{2}dx = x^2 - 3x + C \]

12 – 3 . 1 + C = 0   ⇒ -2 + C = 0    ⇒ C = 2 

F(x) = x2 – 3x + 2 

elrejt
c.) f'(x) = -6x + 5           P (2; 3)

MEGOLDÁS

 

    \[\int -6x + 5\hspace{2}dx = 5x - 3x^2 + C \]

5 . 2 – 3 . 22 + C = 3   ⇒ 10 – 12 + C = 3    ⇒ C = 5

F(x) = 5x – 3x2 + 5 

elrejt
d.) f'(x) = -x + 1           P (-1; 1)

MEGOLDÁS

 

    \[\int -x + 1\hspace{2}dx = x - \frac{x^2}{2} + C \]

    \[(-1) - \frac{(-1)^2}{2} + C = 1 \hspace{2} \Rightarrow \hspace{2}- \frac{3}{2} + C = 1 \hspace{2} \Rightarrow C = \frac{5}{2}\]

    \[F(x) = x - \frac{x^2}{2} + \frac{5}{2} \]

elrejt
e.) f'(x) = 3x2 – 4x           P (0; -4)

MEGOLDÁS

 

    \[\int 3x^2 - 4x \hspace{2}dx = x^3 - 2x^2 + C \]

03 – 2 . 02 + C = -4   ⇒  C = -4 

F(x) = x3 – 2x2 – 4 

elrejt
f.) f'(x) = 6x2 – 5           P (-2; -5)

MEGOLDÁS

 

    \[\int 6x^2 - 5 \hspace{2}dx = 2x^3 - 5x + C \]

2 . -23 – 5 . -2 + C = -5   ⇒  -6 + C = -5 ⇒ C = 1 

F(x) = 2x3 – 5x + 1 

elrejt
g.) f'(x) = -x2 + x + 4           P (3; 4)

MEGOLDÁS

 

    \[\int -x^2 + x + 4\hspace{2}dx = - \frac{x^3}{3} + \frac{x^2}{2} + 4x + C \]

    \[- \frac{3^3}{3} + \frac{3^2}{2} + 4 * 3 + C = 0 \hspace{2} \Rightarrow \hspace{2} 7,5 + C = 4 \hspace{2} \Rightarrow C = -3,5\]

    \[F(x) = - \frac{x^3}{3} + \frac{x^2}{2} + 4x - 3,5 \]

elrejt
h.) f'(x) = 2x3 – 6x           P (-2; 1)

MEGOLDÁS

 

    \[\int 2x^3 - 6x \hspace{2}dx = \frac{x^4}{2} - 3x^2 + C \]

    \[\frac{(-2)^4}{2} - 3 * (-2)^2 + C = 1 \hspace{2} \Rightarrow \hspace{2}-4 + C = 1 \hspace{2} \Rightarrow C = 5\]

    \[F(x) = \frac{x^4}{2} - 3x^2 + 5 \]

elrejt

 

3.) Számítsd ki a következő függvények integrálját a megadott intervallumokon!

a.) f(x) = 2x           [1; 3]

MEGOLDÁS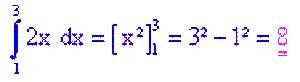

 3.) Számítsd ki a következő függvények integrálját a megadott intervallumokon!

elrejt
b.)

    \[ f(x) = \frac{x}{2} + 1 \hspace{20}[-2; 2]\]

           

MEGOLDÁS

 

    \[\int_{-2}^3 \frac{x}{2} + 1\hspace{2}dx = \Bigg[ \frac{x^2}{4} + x \Bigg]_{-2}^2 = \frac{2^2}{4} + 2 - \Bigg(\frac{(-2)^2}{4} - 2 \Bigg) = 4 \]

elrejt
c.) f(x) =  5 – x           [1; 4]

MEGOLDÁS

 

    \[\int_{1}^4 5 - x \hspace{2}dx = \Bigg[ 5x - \frac{x^2}{2} \Bigg]_{1}^4 = 5 * 4 - \frac{4^2}{2} - \Bigg(5 * 1 - \frac{1^2}{2} \Bigg) = 7,5 \]

elrejt
d.) f(x) =  x2           [1; 3]

MEGOLDÁS

 

    \[\int_{1}^3 x^2 \hspace{2}dx = \Bigg[ \frac{x^3}{3} \Bigg]_{1}^3 = \frac{3^3}{3} - \frac{1^3}{3} = \frac{26}{3} \]

elrejt
e.) 

    \[ f(x) = \frac{x^2}{4} + 2 \hspace{20}[0; 4]\]

    

MEGOLDÁS

 

    \[\int_{0}^4 \frac{x^2}{4} + 2 \hspace{2}dx = \Bigg[ \frac{x^3}{12} + 2x \Bigg]_{0}^4 = \frac{4^3}{12} + 2 * 4 - \Bigg( \frac{0^3}{12} + 2 * 0 \Bigg) = \frac{40}{3} \]

elrejt
f.) 

    \[ f(x) = 4 - \frac{x^2}{3} \hspace{20}[-3; 3]\]

   

MEGOLDÁS

 

    \[\int_{-3}^3 4 - \frac{x^2}{3} \hspace{2}dx = \Bigg[ 4x - \frac{x^3}{9} \Bigg]_{-3}^3 = 4 * 3 - \frac{3^3}{9} - \Bigg( 4 * (-3) - \frac{(-3)^3}{9} \Bigg) = 18 \]

elrejt
g.) f(x) = 4x – x2           [0; 4]

MEGOLDÁS

 

    \[\int_{0}^4 4x - x^2 \hspace{2}dx = \Bigg[ 2 * x^2 - \frac{x^3}{3} \Bigg]_{0}^4 = 2 * 4^2 - \frac{4^3}{3} - \Bigg( 2 * 0^2 - \frac{0^3}{3} \Bigg) = \frac{32}{3} \]

elrejt
h.) f(x) =  x3 + 1         [-1; 1]

MEGOLDÁS

 

    \[\int_{-1}^1 x^3 + 1 \hspace{2}dx = \Bigg[ \frac{x^4}{4} + x \Bigg]_{-1}^1 = \frac{1^4}{4} + 1 - \Bigg( \frac{(-1)^4}{4} - 1 \Bigg) = 2 \]

elrejt
i.) 

    \[ f(x) = \frac{x^3}{4} + 1 - x \hspace{20}[-2; 2]\]

  

MEGOLDÁS

 

    \[\int_{-2}^2 \frac{x^3}{4} + 1 - x \hspace{2}dx = \Bigg[ \frac{x^4}{16} - \frac {x^2}{2} + x \Bigg]_{-2}^2 = \frac{2^4}{16} - \frac{2^2}{2} + 2 - \Bigg( \frac{(-2)^4}{16} - \frac{(-2)^2}{2} - 2 \Bigg) = 4 \]

elrejt
j.) 

    \[ f(x) = \frac{x^3}{4} - \frac{3x^2}{2} + 7 * \frac{x}{2}\hspace{20} [0; 3]\]

  

MEGOLDÁS

 

    \[\int_{0}^3 \frac{x^3}{4} - \frac{3x^2}{2} + 7 * \frac{x}{2} \hspace{2}dx = \Bigg[ \frac{x^4}{16} - \frac {x^3}{2} + \frac{7x^2}{4} \Bigg]_{0}^3 = \]

 

    \[ = \frac{3^4}{16} - \frac{3^3}{2} + \frac{7 * 3^2}{4} - \Bigg( \frac{0^4}{16} - \frac{0^3}{2} + \frac{7 * 0^2}{4} \Bigg) = \frac{117}{16}\]

elrejt
k.) 

    \[ f(x) = \frac{x^4}{4} - 2x^2 + 4 \hspace{20}[-2; 2]\]

   

MEGOLDÁS

 

    \[\int_{-2}^2 \frac{x^4}{4} - 2x^2 + 4 \hspace{2}dx = \Bigg[ \frac{x^5}{20} \Bigg]_{-2}^2 - \frac{2x^3}{3} + 4x + C= \frac{128}{15} \]

elrejt
l.) 

    \[ f(x) = 4 - \frac{1}{x^2} \hspace{20}[0,5; 2]\]

 

MEGOLDÁS

 

    \[\int_{0,5}^2 4 - \frac{1}{x^2} \hspace{2}dx = \Bigg[ 4x +\frac{1}{x} \Bigg]_{0,5}^2 = \frac{9}{2} \]

elrejt
m.) 

    \[ f(x) = x + \frac{1}{x} \hspace{20}[1; 2]\]

 

MEGOLDÁS

 

    \[\int_{1}^2 x + \frac{1}{x} \hspace{2}dx = \Bigg[ 1n x +\frac{x^2}{2} \Bigg]_{1}^2 = 1n 2 +\frac{3}{2} \]

elrejt
n.) 

    \[ f(x) = \sqrt{x} \hspace{20}[0; 9]\]

 

MEGOLDÁS

 

    \[\int_{0}^9 \sqrt{x} \hspace{2}dx = \Bigg[\frac{2x^\frac{3}{2}}{3} \Bigg]_{0}^9 = 18\]

elrejt

 

Területszámítás

4.) Számítsd ki a függvény görbéje és az x tengely által bezárt terület nagyságát!

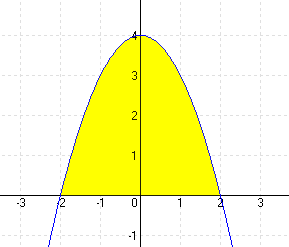
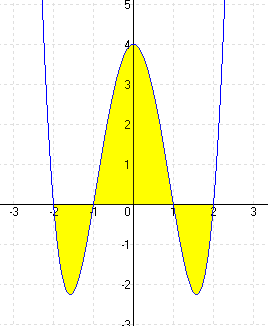
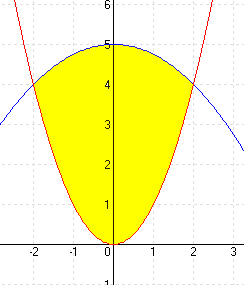
a.) f(x) =  4 – x2   

MEGOLDÁS

4 – x2 = 0       ⇒ x1 = -2    x2 = 2       (A határok) 

    \[ A = \int_{-2}^2 4 - x^2 \hspace{2}dx = \frac{32}{3} \]

 Területszámítás integrál - megoldás 1

elrejt
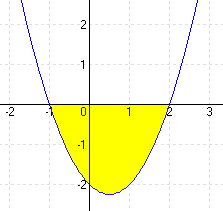
b.) f(x) =  x2 – x – 2   

MEGOLDÁS

x2 – x – 2 = 0       ⇒ x1 = -1    x2 = 3       (A határok) 

    \[ A = \int_{-1}^3 x^2 - x - 2 \hspace{2}dx = \frac{8}{3} \]

 Területszámítás integrál - megoldás 2

elrejt
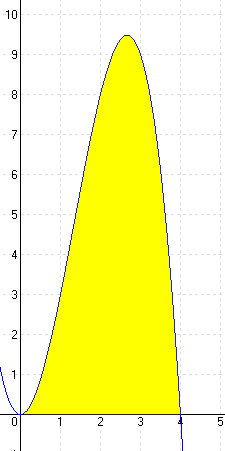
c.) f(x) =  4x2 – x3   

MEGOLDÁS

4x2 – x3 = 0       ⇒ x1 = 0    x2 = 4       (A határok) 

    \[ A = \int_{0}^4 4x^2 - x^3 \hspace{2}dx = \frac{64}{3} \]

 Területszámítás integrál - megoldás 3

elrejt
d.) f(x) =  x3 – 6x2 + 9x   

MEGOLDÁS

x3 – 6x2 + 9x = 0       ⇒ x1 = 0    x2 = 3       (A határok) 

    \[ A = \int_{0}^3 x^3 - 6x^2 + 9x \hspace{2}dx = \frac{27}{4} \]

Területszámítás integrál - megoldás 4 

elrejt
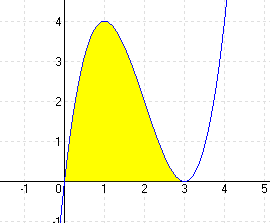
e.) f(x) =  x3 – 6x2 + 8x  

MEGOLDÁS

 x3 – 6x2 + 8x = 0       ⇒ x1 = 0    x2 = 2      x3 = 4 (A határok) 

    \[ \int_{0}^2 x^3 - 6x^2 + 8x \hspace{2}dx = 4\]

 

    \[ \int_{2}^4 x^3 - 6x^2 + 8x \hspace{2}dx = 4\]

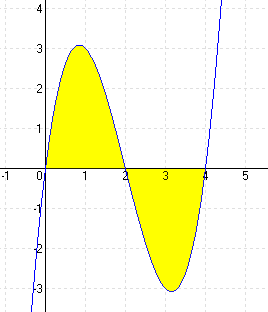
A = 8 Területszámítás integrál - megoldás 5

elrejt
f.) f(x) =  x3 – 8x2 + 15x

MEGOLDÁS

 x3 – 8x2 + 15x = 0       ⇒ x1 = 0    x2 = 3      x3 = 5 (A határok) 

    \[ \int_{0}^3 x^3 - 8x^2 + 15x \hspace{2}dx = \frac{63}{4}\]

 

    \[ \int_{3}^5 x^3 - 8x^2 + 15x \hspace{2}dx = \frac{16}{3} \hspace{25} A = \frac{253}{12}\]

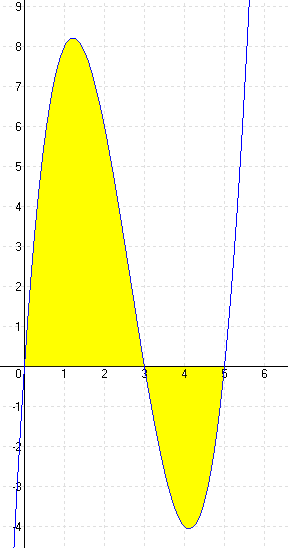
 Területszámítás integrál - megoldás 6

elrejt
g.)

    \[f(x) = \frac{x^3}{3} - 3x\]

MEGOLDÁS

 

    \[\frac{x^3}{3} - 3x = 0 \]

    ⇒ x1 = -3    x2 = 0      x3 = 3 (A határok) 

    \[ \int_{-3}^0 \frac{x^3}{3} - 3x \hspace{2}dx = \frac{27}{4}\]

    \[ \int_{0}^3 \frac{x^3}{3} - 3x \hspace{2}dx = \frac{27}{4} \hspace{25} A = \frac{54}{4}\]

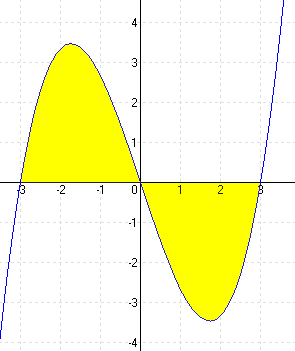
 Területszámítás integrál - megoldás 7

elrejt
h.) f(x) =  x4 – 5x2 + 4

MEGOLDÁS

 x4 – 5x2 + 4 = 0       ⇒ x1 = -2    x2 = -1      x3 = 1      x4 = 2 (A határok) 

    \[ \int_{-2}^{-1} x^4 - 5x^2 + 4 \hspace{2}dx = \frac{22}{15}\]

 

    \[ \int_{-1}^1 x^4 - 5x^2 +4 \hspace{2}dx = \frac{76}{15} \]

    \[ \int_{1}^1 x^2 - 5x^2 +4 \hspace{2}dx = \frac{22}{15} \hspace{25} A = \frac{120}{15} = 8 \]

 Területszámítás integrál - megoldás 8

elrejt

 

5.) Számítsd ki a függvények által közrezárt terület nagyságát!

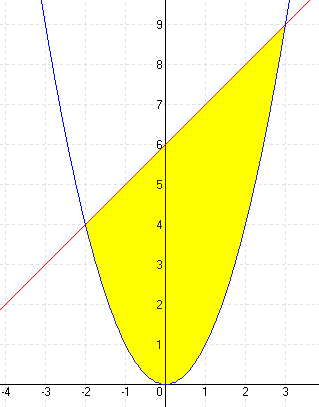
a.) f(x) =  x2         g(x) = x + 6

MEGOLDÁS

 x2 = x + 6      ⇒ x1 = -2    x2 = 3      (A határok) 

    \[ A = \int_{-2}^{3} x^2 - x - 6 \hspace{2}dx = \frac{125}{6}\]

Számítsd ki a függvények által közrezárt terület nagyságát! Feladat 5-1 

elrejt
b.) f(x) =  4x – x2         g(x) = x

MEGOLDÁS

 4x – x2 = x      ⇒ x1 = 0    x2 = 3      (A határok) 

    \[ A = \int_{0}^{3} -x^2 + 3x \hspace{2}dx = \frac{9}{2}\]

 Számítsd ki a függvények által közrezárt terület nagyságát! Feladat 5-2

elrejt
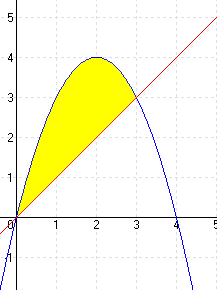
c.) f(x) =  x2         g(x) = 4x – x2

MEGOLDÁS

x2 = 4x – x2      ⇒ x1 = 0    x2 = 2      (A határok) 

    \[ A = \int_{0}^{2} 2x^2 - 4x \hspace{2}dx = \frac{8}{3}\]

Számítsd ki a függvények által közrezárt terület nagyságát! Feladat 5-3 

elrejt
d.)

    \[f(x) = x^2 \hspace{35} g(x) = 5 - \frac{x^2}{4}\]

MEGOLDÁS

 

    \[x^2 = 5 - \frac{x^2}{4} \hspace{8} \Rightarrow x_1 = -2 \hspace{6} x_2 = 2 \]

(A határok) 

    \[ A = \int_{-2}^{2} 5x^2 - 20 \hspace{2}dx = \frac{160}{3}\]

Számítsd ki a függvények által közrezárt terület nagyságát! Feladat 5-4 

elrejt
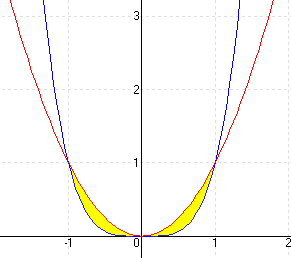
e.) f(x) =  x2         g(x) = x3

MEGOLDÁS

 Mintafeladat volt. 

elrejt
f.) f(x) =  x2         g(x) = x4

MEGOLDÁS

x2 = x4       ⇒ x1 = -1    x2 = 0     x3 = 1 (A határok) 

    \[ \int_{-1}^{0} x^4 - x^2 \hspace{2}dx = \frac{2}{15}\]

    \[ \int_{0}^{1} x^4 - x^2 \hspace{2}dx = \frac{2}{15}\hspace{15} A = \frac{4}{15}\]

Számítsd ki a függvények által közrezárt terület nagyságát! Feladat 5-6

elrejt
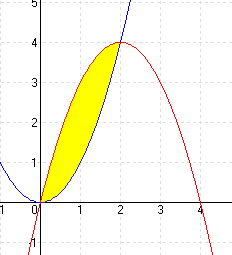
g.) f(x) =  x3 + 1     g(x) = 4x + 1

MEGOLDÁS

x3 + 1 = 4x + 1      ⇒ x1 = -2    x2 = 0     x3 = 2 (A határok) 

    \[ \int_{-2}^{0} x^3 - 4x \hspace{2}dx = 4\]

 

    \[ A = \int_{0}^{2} x^3 - 4x \hspace{2}dx = 4 \hspace{15} A= 8\]

Számítsd ki a függvények által közrezárt terület nagyságát! Feladat 5-7

elrejt
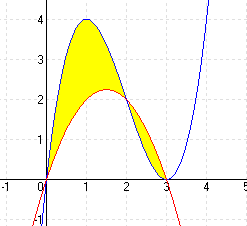
h.) f(x) =  x3 – 6x2 + 9x     g(x) = 3x – x2

MEGOLDÁS

x3 – 6x2 + 9x = 3x – x2      ⇒ x1 = 0    x2 = 2     x3 = 3 (A határok) 

    \[ \int_{0}^{2} x^3 - 5x^2 + 6x \hspace{2}dx = \frac{8}{3}\]

 

    \[ \int_{2}^{3} x^3 - 5x^2 + 6x \hspace{2}dx = \frac{5}{12} \hspace{15} A= \frac{37}{12}\]

Számítsd ki a függvények által közrezárt terület nagyságát! Feladat 5-8

elrejt

 

Térfogatszámítás

1.) Az f(x) függvény egy része (x1; f(x1)) és (x2; f(x2))  pontok között az x tengely mentén forog. Számítsd ki az így keletkező forgástest térfogatát!

a.) f(x) =  3x             x1 = 0              x2 = 2

MEGOLDÁS

y = 3x          x1 = 0           x2 = 2

y2 = 3x

    \[ V_x = \pi \int_{0}^2 9x^2\hspace{2}dx = 9 \pi \Bigg[ \frac{x^3}{3} \Bigg]_{0}^2 = 9 \pi \frac{2^3}{3} = 24 \pi \]

elrejt
b.)

    \[f(x) = \frac{x}{2} + 3 \hspace{10} x_1 = 0 \hspace{5} x_2 = 4 \]

 

MEGOLDÁS

 

    \[ y = \frac{x}{2} + 3 \hspace{15} x_1 = 0 \hspace{5} x_2 = 4\]

    \[ y^2 = \frac{x^2}{4} + 3x + 9 \]

    \[ V_x = \pi \int_{0}^4 \frac{x^2}{4} + 3x + 9 \hspace{2}dx = \pi \Bigg( \frac{1}{4} \Bigg[ \frac{x^3}{3} \Bigg]_{0}^4 + 3 \Bigg[ \frac{x^2}{2} \Bigg]_{0}^4 + 9* \Big[x \Big]_{0}^4 \Bigg)\]

    \[= \pi \Bigg( \frac{1}{4} * \frac{4^3}{3} + 3 * \frac{4^2}{2} + 9 * 4 \Bigg) = \pi \Bigg( \frac{16}{3} + 24 + 36 \Bigg) = 65,33 \pi\]

elrejt
c.) 

    \[f(x) = \frac{x^2}{3} \hspace{10} x_1 = 0 \hspace{5} x_2 = 3 \]

MEGOLDÁS

 

    \[ y = \frac{x^2}{3} \hspace{25} x_1 = 0 \hspace{5} x_2 = 3\]

    \[ y^2 = \frac{x^4}{9} \]

    \[ V_x = \pi \int_{0}^3 \frac{x^4}{9} \hspace{2}dx = \pi \Bigg( \frac{1}{9} \Bigg[ \frac{x^5}{5} \Bigg]_{0}^3 \Bigg) = \Bigg( \frac{1}{9} * \frac{3^5}{5} \Bigg) = \pi \frac{27}{5} = 5,4 \pi\]

elrejt
d.) 

    \[f(x) = x^2 + 1 \hspace{10} x_1 = 0 \hspace{5} x_2 = 2 \]

MEGOLDÁS

 

    \[ y^2 = x^4 + 2x^2 + 1 \]

    \[ V_x = \pi \int_{0}^2 x^4 + 2x^2 + 1 \hspace{2}dx = \pi \Bigg( \Bigg[ \frac{x^5}{5} \Bigg]_{0}^2 + 2 \Bigg[ \frac{x^3}{3} \Bigg]_{0}^2 + 1 \Big[ x \Big]_{0}^2 \Bigg) = \]

    \[\pi \Bigg( \frac{2^5}{5} + 2 \frac{2^3}{3} + 2 \Bigg) = \pi * (6,4 + 5,33 + 2) = 13,73 \pi\]

elrejt
e.) 

    \[f(x) = \sqrt[3]{x} \hspace{10} x_1 = 1 \hspace{5} x_2 = 8 \]

MEGOLDÁS

 

    \[ y^2 = \sqrt[3]{x^2}\]

    \[ V_x = \pi \int_{1}^8 \sqrt[3]{x^2} \hspace{2}dx = \pi \Bigg( \Bigg[\frac{x^\frac{5}{3}}{\frac{5}{3}} \Bigg]_{1}^8 \Bigg) = \pi \Bigg( \frac{3}{5} * 8^{\frac{5}{3}} - \frac{3}{5} * 1\Bigg) = \pi (19,2 - 0,6) = 18,6 \pi\]

elrejt
f.) 

    \[f(x) = \frac{1}{x} \hspace{10} x_1 = 1 \hspace{5} x_2 = 5 \]

MEGOLDÁS

 

    \[ y^2 = \frac{1}{x^2}\]

    \[ V_x = \pi \int_{1}^5 \frac {1}{x^2} \hspace{2}dx = \pi \Bigg( \Bigg[ -\frac{1}{x} \Bigg]_{1}^5 \Bigg) = \pi \Bigg( -\frac{1}{5} + \frac{1}{1} \Bigg) = \pi * \frac{4}{5} = 0,8 \pi\]

elrejt

 

Megtekintés: 9 192


Previous Szigeteken él a súlyosan fenyegetett gerinces fajok csaknem fele
Next Új békafaj, magyar felfedezés 

KAPCSOLÓDÓ BEJEGYZÉSEK

Szöveges feladatok és megoldások
Feladatok függvényvizsgálathoz
Függvények - feladatok és megoldások

10 hozzászólás

  1. Anna
    2023/11/05
    Válasz

    A térfogat számítás első feladatának a megoldókulcsa szerintem félre lett írva. Mert azt írja, hogy y=3x és y²=3x.

  2. krisz
    2023/04/24
    Válasz

    4/b feladatban x1=-1 és x2=2 ( nem 3 ahogy írva van)

    • krisz
      2023/04/24
      Válasz

      ( ez a grafikonon is látszik, a függvény zérushelye -1 és 2.)

  3. Teleki János
    2019/01/13
    Válasz

    A 3/k feladatnál szerintem 128/15 a megoldás. A feladat megoldásánál elmaradt a x^5/20 utáni rész. Ott van még a 2x^3/3 + 4x. Így a teljes behelyettesítés a 2^5/20 – 2×2^3/3 + 4 x 2 – ((-2)^5/20 – 2x(-2)^3/3 + 4 x (-2)) Ezt elvégezve kijön a 128/15 vagy egyszerűsítve a 8 egész 8/15.

  4. Teleki János
    2019/01/13
    Válasz

    Az 1/f feladatban akkor helyes a megoldás, ha a feladat úgy szól, hogy xnégyzet/3+x/4. Így a megoldása xköb/9+2xnégyzet+c

    Amúgy imádom az oldalt, rengeteg jó gyakorlófeladat van fent! Köszönjük a munkájukat!

    • TudományPláza
      2019/01/13
      Válasz

      Kedves János! A megoldás jó volt csak a feladatból maradt ki a perjel 🙂 Köszönjük a jelzést és a dicséretet is. A Szerk.

  5. Iván
    2018/11/29
    Válasz

    Az g) feladat: x^4/10-3x^2+2/3 megoldása hibás.
    A helyes megoldás: x^5/50-x^3+2/3x+c

Leave a reply

Az e-mail címet nem tesszük közzé. A kötelező mezőket * karakterrel jelöltük

3 × öt =