Másodfokú függvények

Olvasási idő: < 1 perc

$f : y = ax^2 + bx + c (a, b, c\in \mathbb{R},$

ahol a nem lehet nulla, másodfokú függvénynek nevezzük.

A függvény képe egy parabola, melynek tengelypontja az origó.

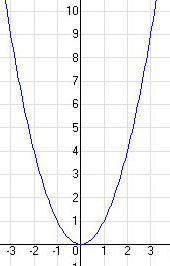
Eltolási szabályok

Az x² + b ( illetve x² – b) függvény képe előállítható, ha az x²-et b-vel felfelé (illetve lefelé) eltoljuk.	Az (x + c)² (illetve (x – c)²) függvény képe előállítható, ha az x²-et c-vel balra (illetve jobbra) eltoljuk.
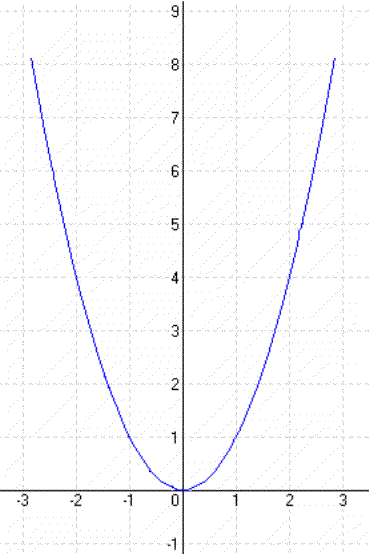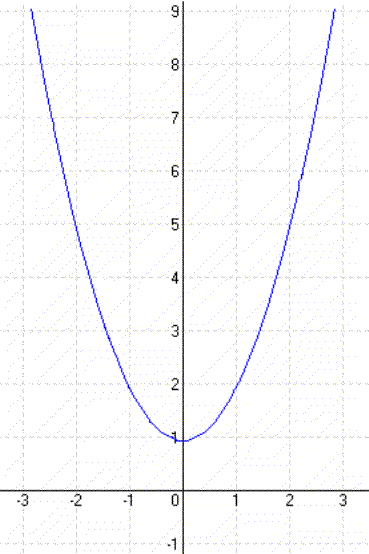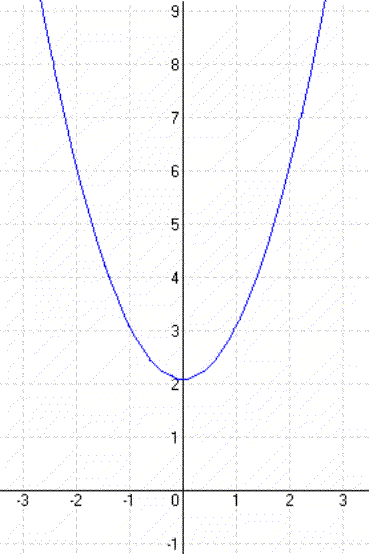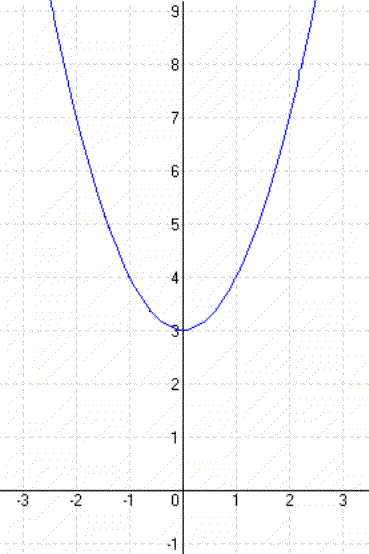
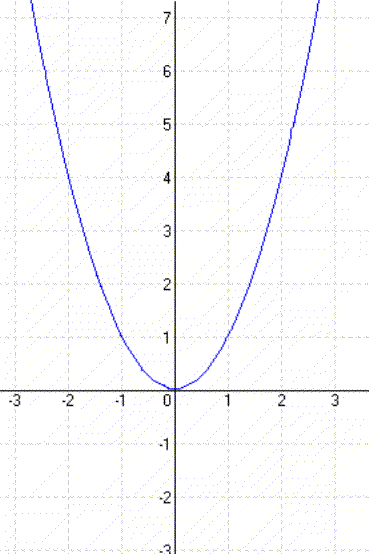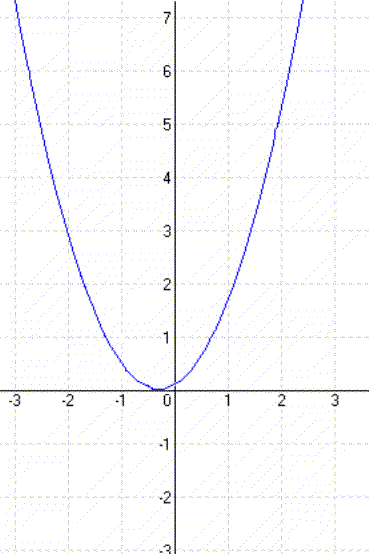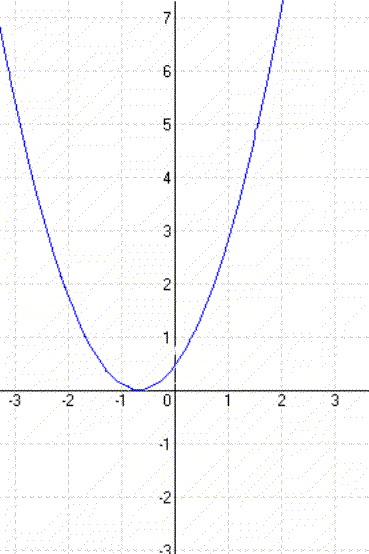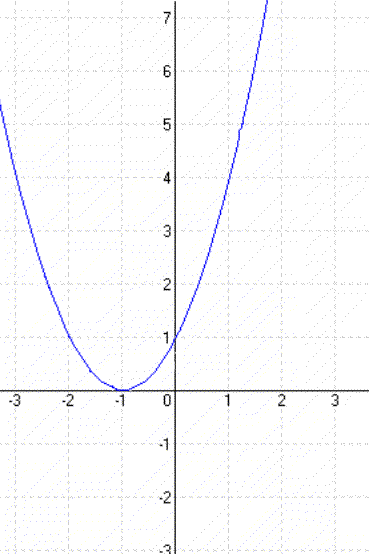
Példa: y = x² + 3	Példa: y = (x – 2)²

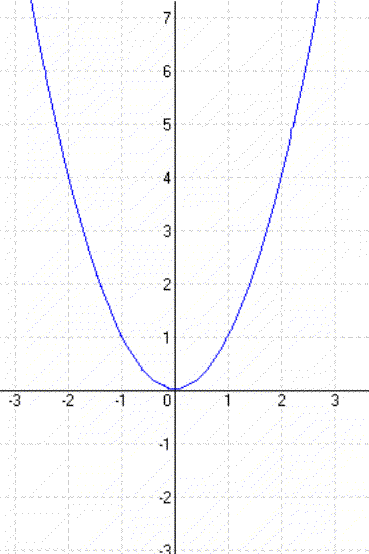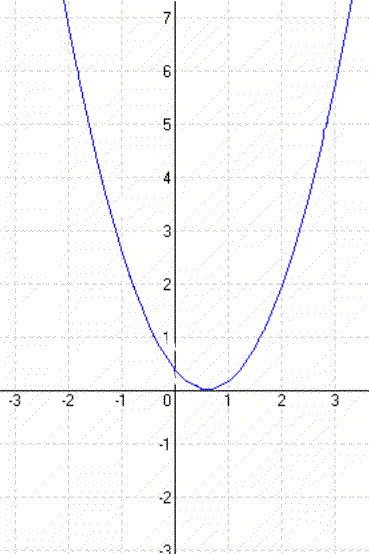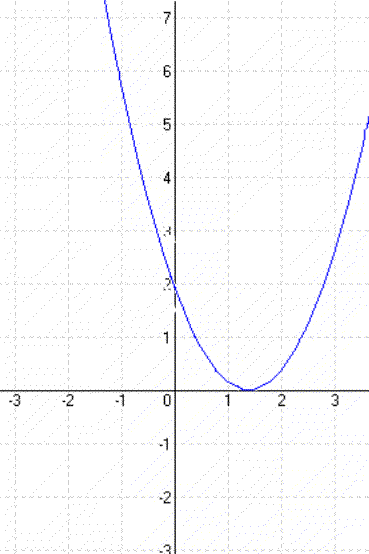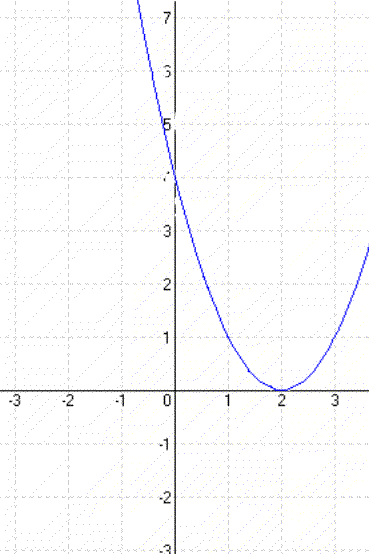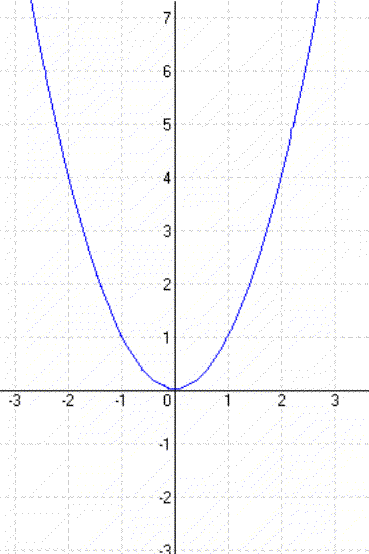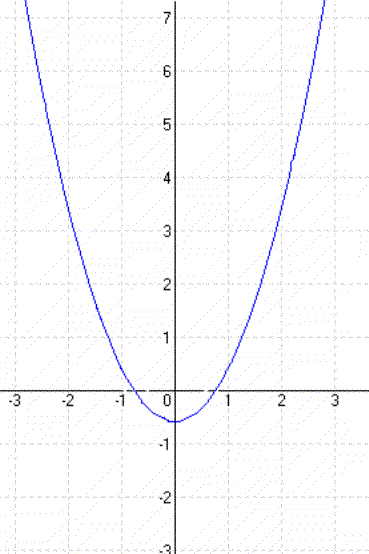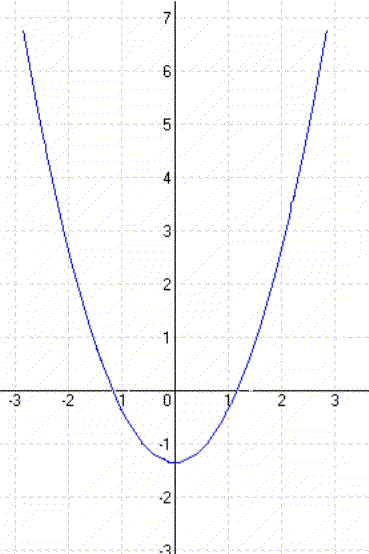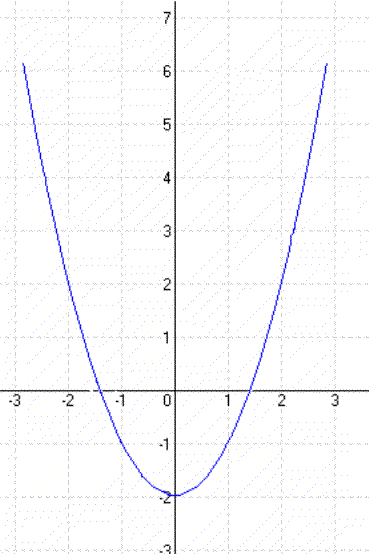
y = x² – 2	y = (x + 1)²

Minden másodfokú függvény egyenlete teljes négyzetté való alakítással a következő formára hozható:
y = x² – 10x + 24 = x² – 10x + 25 – 25 + 24 = (x – 5)² -1

Tehát a normál parabola 5 egységgel jobbra (pozitív irányba!), valamint 1 egységgel lefelé lett eltolva.

A parabola tengelypontja: T(5;- 1).

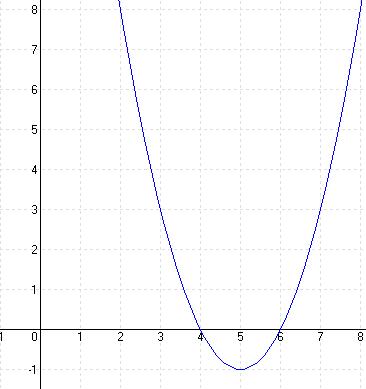
Ha az egyenletet egy konstanssal szorozzuk meg, akkor a függvény képe az y irányban „soványabb” illetve „kövérebb” lesz. A (-1)-gyel való szorzással az x tengelyre tükröződik a parabolánk (alulról nyitott).

A következőket foglalhatjuk össze:

a másodfokú függvény	f : y = ax² + bx + c = a(x – b)² + c
képe	parabola
a
b	ha b > 0, akkor a negatív irányba (balra) b-vel az x tengely mentén eltoljuk ha b < 0, akkor a pozitív irányba (jobbra) b-vel az x tengely mentén eltoljuk
c	y tengellyel való metszéspont
tengelypont (b;c)	Vigyázat(!): pl.: (x + 5)² + 6 S(-5;6) (x – 3)² + 9 S(3;9)