A Születésnap-paradoxon lényegében egy valószínűségszámítási feladat, ami megmutatja: hiedelmeink sokszor tévútra visznek minket a számok világában.

Talán Önnel is előfordult iskolásként, hogy egy osztálytársának ugyanarra a napra esett a születésnapja. Gyerekként ilyenkor izgalomba jöttünk, úgy gondoltuk a valószínűtlen esemény egy kész csoda. Amíg nem gondoljuk át alaposan a problémát, sokszor felnőttként is megdöbbenhetünk egy ilyen „véletlenen”. A matematika ezt Születésnap-paradoxonnak nevezi.

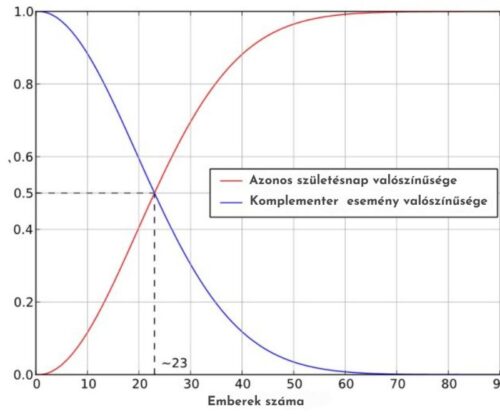
A Születésnap-paradoxon azt hivatott bizonyítani, hogy egy kisebb csoport, egy helyiségben tartózkodó ember között – a példa kedvéért 23 ember – viszonylag nagy valószínűséggel lesz két fő, akiknek egyezik a születésnapja. A probléma valójában nem tartalmaz logikai ellentmondást, így ilyen értelemben nem paradoxon. A név arra utal, hogy – az emberek hiedelme szerint – általában ennek kevés az esélye. Feltételezhetően Harold Davenport dolgozta ki a problémát először.

A vizsgált kérdés:

Mekkora a valószínűsége annak, hogy egy szobában tartózkodó 23 ember közül kettőnek ugyanarra a napra esik a születésnapja?

A megoldás egyszerűbb levezetéséhez feltételezzük a következőt: statisztikailag minden szobában tartózkodó személy születésnapja egyenlő eséllyel esik az év bármelyik napjára. Ez valójában hamis, de ez nincs hatással a hiedelmeinkre és a probléma relevanciájára.

A Születésnap-paradoxon kiszámoláshoz egy általánosan ismert valószínűségszámítási módszert, a komplementer esemény meghatározását használjuk. Tehát, azt számoljuk ki mennyi az esélye annak, hogy a vizsgált esemény nem következik be, azaz nincs két személy a szobában azonos születésnappal.

Ha n jelöli a szobában tartózkodók számát a komplementer valószínűséget így tudjuk kiszámolni:

A második személy születésnapja más kell legyen, mint az elsőnek (364/365), a harmadiknak más kell legyen, mint az első kettőnek és így tovább az n-dik emberig.

Vegyük a példában említett esetet, tehát a 23 fős osztályt! Ez esetben:

Annak az esélye, hogy mindannyiuk születésnapja különböző napokra esik, tehát körülbelül 49,3%. Ez a komplementer valószínűség, ezt kell kivonnunk 1-ből, hogy megkapjuk a választ az eredeti kérdésünkre.

1-0,4927=0,5073

Megkaptuk a megoldást: annak a valószínűsége, hogy egy 23 fős szobában van két fő, akiknek ugyanarra a napra esik a születésnapjuk, 50,73%. Ez után már nem hangzik olyan csodásnak, ugye?

Ha szívesen olvasnál még matematikáról kövesd a Facebook-oldalunkat!