Ha az egyenlet

ax³ + bx² + cx + d = 0

illetve

x³ + pk² +qx +r =0

alakú, akkor harmadfokú egyenletről beszélünk.

A harmadfokú egyenlet általános megoldóképlete nagyon bonyolult, és emellett gyakorlatban is alig használják. De egynéhány esetben egy harmadfokú egyenletet vissza tudunk vezetni egy másodfokúra.

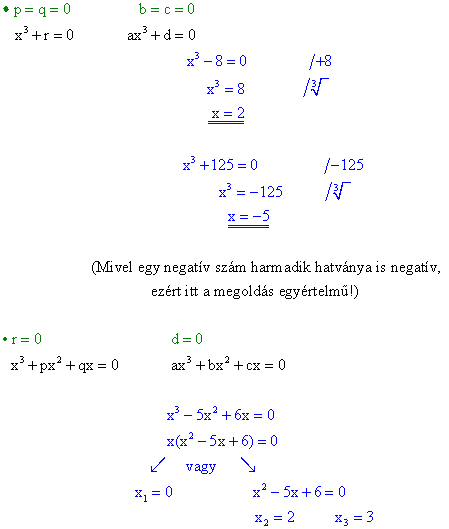
Az egyenletet felbontottuk egy lineáris és egy másodfokú egyenlet szorzatára. Ezt így már meg tudjuk oldani.

Ha egy gyök ismert (korábban megadták, vagy próbálgatás során kaptuk meg)

A Viéte-formula létezik magasabb fokú egyenletekre is. Tehát, ha egy harmadfokú egyenlet megoldásai x₁, x₂ és x₃, akkor 

x³ + px² + qx + r = (x – x₁) . (x – x₂) . (x – x₃)

Ha például ismerjük x₁-et, akkor az egyenlet bal oldalát (x – x₁)-gyel eloszthatjuk és így egy másodfokú egyenletet kapunk.

Ha egyáltalán létezik megoldás az egész számok halmazán, akkor az abszolút r tag osztója kell, hogy legyen.

Példa:

x³ – 4x² + x + 6 = 0

Lehetséges megoldások az egész számok közül:

+1; +2; +3; +6

Próbálgatás útján megkapjuk x₁ = 2

(x³ – 4x² + x + 6) : (x – 2) = x² – 2x – 3

x² – 2x – 3 = 0         ⇒ x₂ = -1;         x₃ = 3

Az úgynevezett Horner-elrendezéssel a próbálgatást és az osztást egy lépésben összefoglalhatjuk.