
A háromszögek fajtái
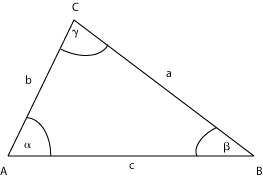
A háromszög egy olyan sokszög, melynek három oldala van. A három oldalból következően pedig három csúcsa is van. A csúcsokat nagybetűvel (A, B, C) szokták jelölni.
A háromszög oldalait kisbetűvel (a,b,c) jelöljük. Az erre vonatkozó szabály szerint úgy, hogy az A csúccsal szemközti oldalt a-val, a B csúccsal szemközti oldalt b-vel, a C csúccsal szemközti oldalt pedig c-vel.
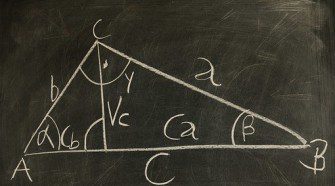
Egyéb területképletek háromszögekhez
Kis háttér-kiegészítésként elmondható, hogy a Heron-képlet vagyis a sokak által Hérón-képletnek nevezett formula az Alexandriában élt Héron görög matematikusról kapta a nevét, mert ő bizonyította elsőként.
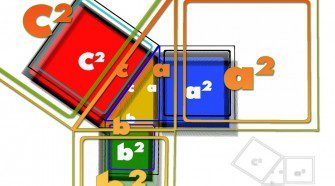
Pythagoras tétele
Minden derékszögű háromszögben a befogók négyzetösszege egyenlő az átfogó négyzetével. Bizonyítás: 1. Terület c2 = a2 + b2 2. Szög α + β + γ = 180 ° γ = 90 ° Megtekintés: 457
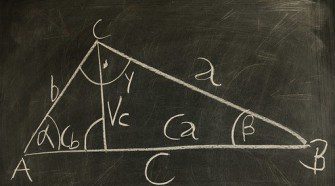
Magasságtétel és befogótétel
Magasságtétel Minden derékszögű háromszögben az átfogó magasságának a talppontja az átfogót két olyan részre bontja, melyeknek a magasság a mértani közepe. h2 = pq Befogótétel Minden derékszögű háromszögnek egy befogója mértani közepe az átfogónak és a befogó átfogóra eső vetületének. a2 = cq b2 = cp Megtekintés: 8 392

Thalész-kör
Maga a tétel a következőket mondja ki:
Az ABC derékszögű háromszög C csúcsánál derékszög van, ha a C pont az AB szakasz mint átmérő fölé írt félkörön van, kivéve az A és B pontokat.
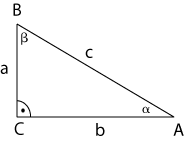
Sinus és cosinus a derékszögű háromszögben
A trigonometria a matematika egy ága, amely a geometrián belül a derékszögű háromszögek oldalai és szögei közötti összefüggésekkel foglalkozik. c = átfogó a és b = befogó Megtekintés: 43 686
Sinus- és cosinustétel minden háromszögben
Sinustétel Cosinustétel c2 = a2 + b2 – 2ab . cos γ a2 = b2 + c2 – 2bc . cos α b2 = a2 + c2 – 2ac . cos β Megtekintés: 1 408
Háromszög magasságpont
Egy háromszög magasságvonalán a háromszög egyik csúcsából a szemközti oldal egyenesére bocsátott merőlegest értjük.
Egybevágósági alapesetek
Két háromszög hasonló, ha a következő feltételek egyike teljesül, illetve ha a következő adatok adottak, akkor a háromszög szerkeszthető!
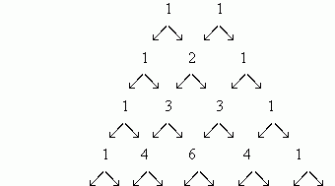
Pascal-háromszög
Egy végtelenül folytatható számtáblázatról és annak kombinatorikai jelentőségéről először Blaise Pascal értekezett.


