
Megoldási séma szélsőértékfeladathoz
A gyakorlatban gyakran állunk szemben olyan feladattal, hogy egy mennyiséget (terület, felszín, térfogat, anyagfelhasználás, költség stb.) optimalizálnunk kell.
Ha a mennyiséget egy egyváltozós függvénnyel kifejezhetjük, akkor az 1. derivált segítségével kiszámíthatjuk a szélsőértéket. Ha több változó fordul elő, akkor ezeket először ki kell fejezni egy változó segítségével.

A differenciálhányados
Probléma Keressük az f függvény változását az x helyen. Geometriai szemléltetés Az érintő meredeksége a P(x ; f(x)) pontban: A P, Q pontokon átmenő szelő (zöld vonal) meredeksége: Ezt a kifejezést nevezzük DIFFERENCIAHÁNYADOSNAK. Minél jobban közeledik a Q pont a P ponthoz, annál meredekebb a szelő. Mikor P és Q egybeesik, a …
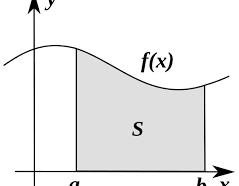
Primitív függvények (Határozatlan integrál)
Az analízis legfontosabb részterülete az integrálszámítás. Ha a primitív függvényeket vizsgáljuk rögtön egy definícióval kezdhetjük.

A 2. derivált jelentése
A 2. derivált jelentése – A 2. derivált a meredekség változását adja meg. Tehát információt tudhatunk meg a függvény görbületeiről.

Fordított feladatok függvényvizsgálathoz
Ezeknél a feladatoknál a függvény egyenletét kell megkeresni néhány megadott pont alapján. Írjuk először fel a függvények általános egyenletét! Például Harmadfokú polinomfüggvény: f(x) = ax3 + bx2 + cx + d Negyedfokú polinomfüggvény: f(x) = ax4 + bx2 + c (ez szimmetrikus az y tengelyre nézve!) (A szimmetria miatt a páratlan kitevők elhagyhatóak.) Ezekből képezzük …

Szimmetria-tulajdonságok
Ha x csak páros kitevővel fordul elő (esetleg még konstansok is vannak), akkor a következő érvényes minden x-re: f(-x) = f(x) Az ilyen függvényt páros függvénynek nevezzük. A függvény szimmetrikus az y-tengelyre. Ha x csak páratlan kitevővel fordul elő, akkor a következő érvényes minden x-re: f(-x) = – f(x) Az ilyen függvényt páratlan …

Függvények alapfogalmai
Egy függvény tulajdonképpen egy hozzárendelés, amely során az értelmezési tartomány minden eleméhez pontosan egy elemet rendelünk az értékkészletből. Az értelmezési tartomány elemét – az argumentet, illetve a független változót – x-szel szokás jelölni, az értékkészletből hozzárendelt elemet – a függvényértéket, illetve a függő változót – pedig y-nal. Argument – független változó – x Függvényérték – …

Implicit függvények
Adott a következő egyenlettel egy függvény: x + y = 5 (minden x értékhez pontosan egy y érték tartozik.) Ezt a fajta függvény megadási módot nevezzük implicit függvény megadásnak. Az explicit függvénymegadást úgy kapjuk meg, ha az egyenletet y-ra átrendezzük: y = 5 – x Megtekintés: 546

Másodfokú függvények
Az f : y = ax² + bx + c (a, b , c e R, ahol a nem lehet nulla) másodfokú függvénynek nevezzük.
Exponenciális és logaritmusfüggvény
A felsőbb matematikában legtöbbször a „természetes alapú exponenciális függvényt” alkalmazzák. Ez az a függvény, melynek meredeksége a (0;1) pontban 1.


