Adott az f(x) függvény; szeretnénk kiszámolni az [a; b] intervallumban a függvény és az x tengely közti területet.
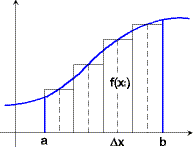
A közelítőértéket úgy kapjuk meg, ha [a; b] intervallumot részintervallumokra bontjuk, melyek nagysága Δx. Majd minden részintervallumban az xi értékhez tartozó függvényértéket megszorozzuk a Δx-szel ( Δx . f(xi)), majd összeadjuk őket. Ez ugyanis a részintervallumok (téglalapok) területe.
A ≈ (f(x1) + f(x2) + … + f(xn)) . Δx
összeg-írásmód:
![\[A \approx \sum_{i = 1}^n{}f(x_i) * \Delta x\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-94b26597ce4cc219b18bbce885ab7a10_l3.png "Rendered by QuickLaTeX.com")
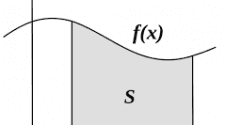
A területet – azaz a határozott integrált – az összeg határértékeként definiáljuk, ha Dx nullához tart. Írásmódok:
![\[ A = \int_{a}^b f(x) dx\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-2d59cb0cc8e89eff3ef344040c86f45b_l3.png "Rendered by QuickLaTeX.com")
ejtsd „Integrál a-tól b-ig f(x) dx”
No Comment