A differenciálszámítás segítségével függvényvizsgálatot tudunk végezni:

– Hol növekvő, illetve csökkenő a függvény.
– Hol vannak a nevezetes pontjai mint:

• maximuma,
• minimuma,
• inflexiós pontja.

Megjegyzés 1.

• Ha egy függvényértéket egy adott x helyen keresünk, akkor x-et az EREDETI függvénybe kell behelyettesítenünk.
• Ha a meredekséget egy adott helyen keressük, akkor x-et az 1. DERIVÁLTBA helyettesítjük.

Megjegyzés 2. (profiknak)

f(x) alatt a következőkben mindig egy kétszer, folytonosan differenciálható függvényt értünk.

Az 1. derivált a függvényértékek változását adja meg, azaz a függvény meredekségét egy meghatározott helyen.

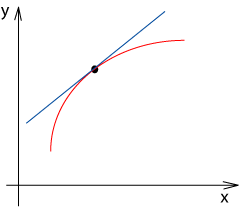
Ha f ‘(x) > 0, akkor a függvény
monoton növekvő.

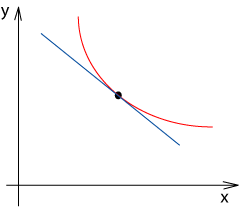
Ha f ‘(x) < 0, akkor függvény
monoton csökkenő.

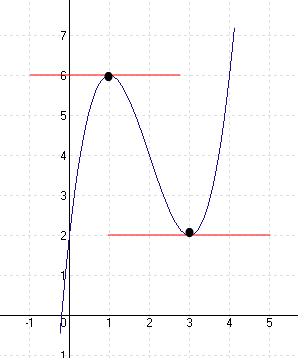
Ha f ‘(x)=0, akkor a függvénynek ezen a helyen egy vízszintes érintője van.

Ez lehet a maximuma vagy a minimuma a függvénynek …

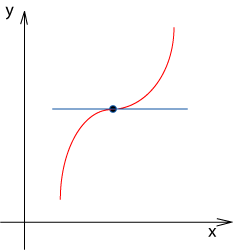
… de lehet egy inflexiós pontja egy vízszintes érintővel.

Hogy ezt eldöntsük, szükségünk lesz a 2. deriváltra.