A változó (a, b, x, …) egy számnak tartja fent a helyét.

Egy algebrai kifejezés mindig számokból, változókból és műveleti jelekből áll.

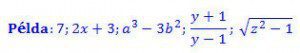
Egy algebrai kifejezés értelmezési tartománya: minden olyan szám, amelyek a változókba helyettesíthetőek. Emellett ügyelnünk kell például arra is, hogy egy törtkifejezésben a nevező soha nem lehet 0.

Ha egy kifejezésben szereplő változók helyére számokat írunk, akkor egy bizonyos értéket kapunk (ezt nevezzük ismert nevén behelyettesítésnek).

Példa:
T(x) = 2x + 3                           D = {1; 2; 3; 4; 5}

x                              T(x)
1                        2 · 1 + 3 = 5
2                       2 · 2 + 3 = 7
3                       2 · 3 + 3 = 9
4                       2 · 4 + 3 = 11
5                       2 · 5 + 3 = 13

Két algebrai kifejezést ekvivalensnek nevezünk, ha minden behelyettesítés során ugyanazt az értéket veszik fel.

Példa: 2x + 3x = 5x

Ezentúl mindig arra fogunk törekedni, hogy minden algebrai kifejezést egy vele ekvivalens, egyszerűbb formába hozzunk.

Monom: egytagú algebrai kifejezés pl.: 2ab
Polinom: többtagú algebrai kifejezés pl.: x³+2x²-4x-1
Együtthatók: számok, amelyekkel a változók meg vannak szorozva (itt: 1; 2; -4)
Polinom foka: az algebrai kifejezésben előforduló legmagasabb kitevő.

A kéttagú algebrai kifejezéseket szokás hivatalosan binomnak is mondani. Ezenkívül vannak még algebrai törtkifejezések, gyökkifejezések és a többi.