Egyismeretlenes egyenletek
Az A(x) = B(x) kifejezést egyenletnek nevezzük, ahol x az ismeretlen. A és B tetszőleges algebrai kifejezések. (Az ismeretlent természetesen jelölhetjük más betűvel is!) Alaphalmaz: minden olyan szám, ami az egyenletbe behelyettesíthetőnek tűnik. (jelölése: A) Definícióhalmaz: minden elem az alaphalmazból, amelyet az egyenletbe helyettesíthetünk. (jelölése: D) Megoldáshalmaz: minden elem a definícióhalmazból, amelyet az egyenletbe helyettesítve …
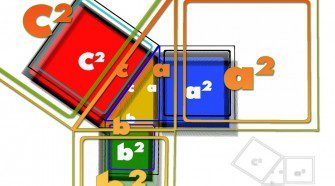
Pythagoras tétele
Minden derékszögű háromszögben a befogók négyzetösszege egyenlő az átfogó négyzetével. Bizonyítás: 1. Terület c2 = a2 + b2 2. Szög α + β + γ = 180 ° γ = 90 ° Megtekintés: 446
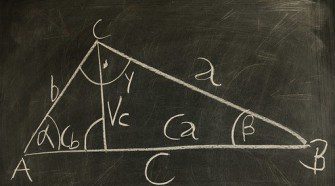
Magasságtétel és befogótétel
Magasságtétel Minden derékszögű háromszögben az átfogó magasságának a talppontja az átfogót két olyan részre bontja, melyeknek a magasság a mértani közepe. h2 = pq Befogótétel Minden derékszögű háromszögnek egy befogója mértani közepe az átfogónak és a befogó átfogóra eső vetületének. a2 = cq b2 = cp Megtekintés: 8 293
Ekvivalens átalakítások
Egy egyenlet megoldáshalmaza nem változik, ha mindkét oldalát a következőképpen változtatjuk: ugyanazt a számot (kifejezést) adjuk, illetve vonjuk ki mindkét oldalból ugyanazzal a számmal (kifejezéssel) (szám, illetve kifejezés nem lehet nulla) megszorozzuk mindkét oldalt ugyanazzal a számmal (kifejezéssel) (szám, illetve kifejezés nem lehet nulla) osztjuk mindkét oldalt. Mindig megpróbálunk egy egyenletet ekvivalens átalakításokkal a lehető …
Diszkrimináns
ha D > 0, két megoldása van az egyenletnek, ha D = 0, egy megoldása van az egyenletnek, ha D < 0, egy valós megoldása sincs az egyenletnek. Megtekintés: 256
Harmadfokú egyenletek
A harmadfokú egyenlet általános megoldóképlete nagyon bonyolult, és emellett gyakorlatban is alig használják. De egynéhány esetben egy harmadfokú egyenletet vissza tudunk vezetni egy másodfokúra.
Horner-elrendezés
A Horner-elrendezés (William George Horner, 1786-1837) segítségével ki tudjuk a polinom értéket számolni, és egyúttal el tudjuk osztani a polinomot egy lineáris faktorral.
