
Fordított feladatok függvényvizsgálathoz
Ezeknél a feladatoknál a függvény egyenletét kell megkeresni néhány megadott pont alapján. Írjuk először fel a függvények általános egyenletét! Például Harmadfokú polinomfüggvény: f(x) = ax3 + bx2 + cx + d Negyedfokú polinomfüggvény: f(x) = ax4 + bx2 + c (ez szimmetrikus az y tengelyre nézve!) (A szimmetria miatt a páratlan kitevők elhagyhatóak.) Ezekből képezzük …
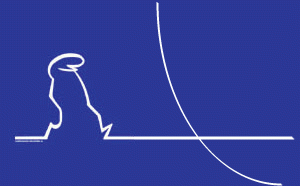
A függvény nevezetes pontjai
Összefoglalva: Metszéspontok az y-tengellyel x = 0 Zérushelyek (metszéspontok az x-tengellyel) f(x) = 0 (y =0) Szélsőértékhelyek f'(x) = 0 A megtalált értéket behelyettesítve 2. deriváltba: f”(x) < 0: maximum f”(x) > 0: minimum Inflexiós pontok f”(x) = 0; f”'(x) ≠ 0 Az inflexiós pontba húzott érintőt megkapjuk, ha a kapott értéket behelyettesítjük az 1. deriváltba. Megtekintés: 497

Szimmetria-tulajdonságok
Ha x csak páros kitevővel fordul elő (esetleg még konstansok is vannak), akkor a következő érvényes minden x-re: f(-x) = f(x) Az ilyen függvényt páros függvénynek nevezzük. A függvény szimmetrikus az y-tengelyre. Ha x csak páratlan kitevővel fordul elő, akkor a következő érvényes minden x-re: f(-x) = – f(x) Az ilyen függvényt páratlan …
Mintafeladat a függvényvizsgálathoz
Add meg a függvény tengelyekkel való metszéspontjait, a szélsőértékeket, az inflexiós pontokat, valamint az inflexiós pontba húzott érintő egyenletét! Megoldás: Képezzük először a deriváltakat! a.) tengelyekkel való metszéspontok: » Metszéspontok az x-tengellyel: Zérushelyek: f(x)=0 Horner elrendezéssel kiszámoljuk a zérushelyeket: Együtthatók …
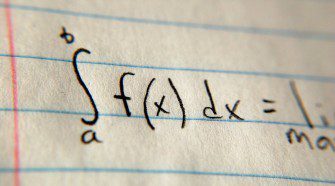
Az integrálszámítás szabályai
Példa: Egy függvény deriváltja a következő: f'(x) = 2x; A függvény átmegy a P (2; 7) ponton. P koordinátáit behelyettesítve: 22 + C = 7 ⇒ C = 3 f(x) = x2 + 3 Megtekintés: 479
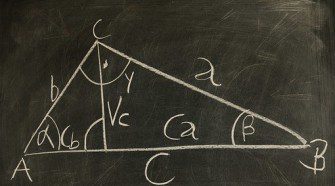
Egyéb területképletek háromszögekhez
Kis háttér-kiegészítésként elmondható, hogy a Heron-képlet vagyis a sokak által Hérón-képletnek nevezett formula az Alexandriában élt Héron görög matematikusról kapta a nevét, mert ő bizonyította elsőként.

Deriválási szabályok
Fontosabb függvények deriváltjai: y = f(x) y’ = f'(x) c (konstans) 0 xn n . xn-1 sinx cosx cosx -sinx ex ex lnx Deriválási szabályok: A szabály neve Függvény Derivált Konstans-szabály y = c . f(x) y’ = c . f'(x) Összeg-szabály y = f(x) ± g(x) y’ = f'(x) ± g'(x) Szorzat-szabály y …

A határozott integrál
Adott az f(x) függvény; szeretnénk kiszámolni az [a; b] intervallumban a függvény és az x tengely közti területet.
Mintafeladatok
1.) y = 4×3 + 5×2 – 3x + 2 y’ = 4 . 3×2 + 5 . 2x – 3 = 12×2 + 10x – 3 2.) 3.) 4.) y = (x2 + 1) . sin x y’ = (x2 + 1)’ …
A differenciál- és integrálszámítás főtétele
ez azt jelenti, hogy az f(x) függvény képe alatti terület f primitív függvénye.


