Figyelem: Az f(x) < 0 értékekre az integrál szintén negatív. A függvény görbéje és az x tengely közötti terület lesz az integrál.
- Ha a függvény a megadott intervallumon egy vagy több zérushellyel rendelkezik, akkor az egyes területeket külön-külön kell kiszámolni, majd ezeket összeadni.
- Ha a függvény görbéje és az x tengely közötti területet úgy kell meghatározni, hogy semmilyen intervallum nincs megadva, akkor előbb meg kell határoznunk a zérushelyeket – ezek lesznek az integrációs határok.
- Két függvény f(x) és g(x) közti területet a következő képlettel lehet kiszámolni:
![\[ A = \int_{x_1}^{x^2} (f(x) - g(x))dx\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-27e8ae33a43c721bdfc776443fbdbe51_l3.png "Rendered by QuickLaTeX.com")
Az integrációs határ (határok) a két függvény metszéspontjának x koordinátája (koordinátái). Ha több mint két metszéspontjuk van, akkor ismét az egyes területeket külön-külön kell kiszámolni.
Példa:
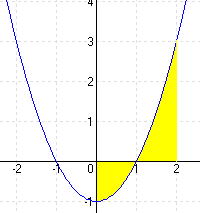
1.) Mekkora az f(x) = x² – 1 függvény x tengellyel bezárt területe a = 0 és b = 2 között?
A függvénynek x1 = 1-nél zérushelye van, tehát 0-tól 1-ig, majd 1-től 2-ig kell integrálnunk.
![\[ \int_{0}^{1} (x^2 - 1) dx = \Bigg[ \frac{x^3}{3} - x \Bigg]^1_0 = -\frac{2}{3}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-913ff2e45ca891230585c3a0a14d4290_l3.png "Rendered by QuickLaTeX.com")
![\[ \int_{1}^{2} (x^2 - 1) dx = \Bigg[ \frac{x^3}{3} - x \Bigg]^2_1 = -\frac{4}{3}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-07d9207896f12b56b5c3961287b2206c_l3.png "Rendered by QuickLaTeX.com")
![\[ A = \frac{2}{3} + \frac{4}{3} = 2\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-290d6d6c8e317d4169fc052d9d80237a_l3.png "Rendered by QuickLaTeX.com")
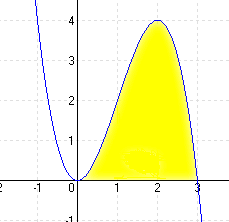
2.) Mekkora az f(x) = -x³+ 3x² függvény x tengellyel bezárt területe?
Zérushelyek meghatározása, -x3 + 3x2 = o ⇒ x2 (-x + 3) = 0
x1 = 0 -x + 3 = 0 ⇒ x2 = 3
![\[ A = \int_{0}^{3} (-x^3 + 3x^2) dx = \Bigg[ -\frac{x^4}{4} + x^3 \Bigg]^3_0 = 6\frac{3}{4}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-0ffe9a97dd8d6c29a56b0fce2fda6694_l3.png "Rendered by QuickLaTeX.com")
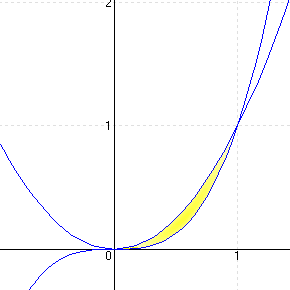
3.) Mekkora az f(x) = x² és g(x) = x³függvények által bezárt terület nagysága?
Metszéspontok meghatározása,
x2 = x3 ⇒ x3 – x2 = 0 ⇒ x2 (x – 1) = 0
x1 = 0 x – 1 = 0 ⇒ x2 = 1
![\[ A = \int_{0}^{3} (x^3 - x^2) dx = \Bigg[ \frac{x^3}{3} - \frac{x^4}{4}\Bigg]^1_0 = \frac{1}{12}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-2a45b3fe96d7b6f76434c44625e5c815_l3.png "Rendered by QuickLaTeX.com")
No Comment