Vizsgáld meg és rajzold fel a következő függvények képét! (Zérushelyek, szélsőértékek, inflexiós pont, az inflexiós pontba húzott érintő egyenlete.)
| 1.) f(x) = x2 – x – 2 |
|
MEGOLDÁS
f'(x) = 2x – 1 f”(x) = 2 f”'(x) = 0
2. lépés: Zérushelyek f(x) = 0 x2 – x – 2 = 0 N1 (2; 0) N2 (-1; 0)
Metszéspontok a tengellyel: x = 0 y = 02 – 0 – 2 = -2 Sy (0; -2)
3. lépés: Szélsőértékek: f'(x) = 0
Kérdés: maximum vagy minimum? f”(x) < o maximum f”(x) > o minimum
4. lépés: Inflexiós pont nincs.
elrejt |
| 2.) f(x) = x3 – 6x2 + 9 |
|
MEGOLDÁS 1. lépés: Deriváltak képzése f'(x) = 3x2 – 12x + 9 f”(x) = 6x – 12 f”'(x) = 6
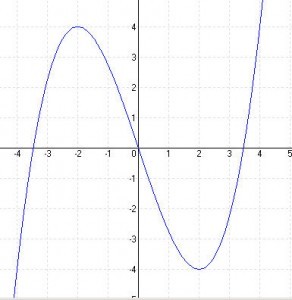
2. lépés: Zérushelyek f(x) = 0 Horner-elrendezéssel N1 (3; 0) N2 (0; 0)
Metszéspontok a tengellyel: x = 0 y = 03 – 6 . 02 – 9 . 0 = 0 Sy (0; 0)
3. lépés: Szélsőértékek: f'(x) = 0 3x2 – 12x + 9 = 0 ⇒ x1 = 3 x2 = 1 y1 = 0 y2 = 4 E1 (3; 0) = min E2 (1; 4) = max
Kérdés: maximum vagy minimum? f”(x) < o maximum f”(x) > o minimum f”(x1) = f”(3) = 6 > 0 minimum = min f”(x2) = f”(1) = -6 < 0 maximum = max
4. lépés: Inflexiós pont: f”(x) = 0 6x – 12 = 0
Inflexiós pontba húzott érintő egyenlete: k = f'(x)
elrejt |
| 3.)
|
|
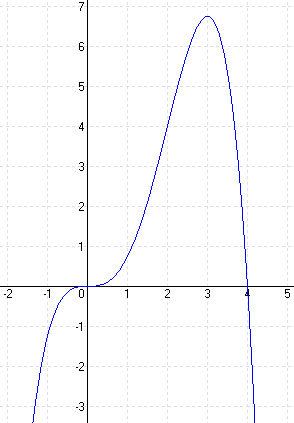
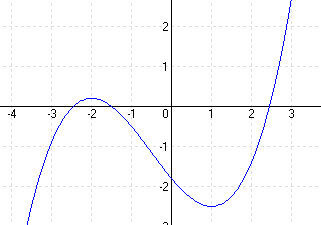
MEGOLDÁS 1. lépés: Deriváltak képzése f'(x) = -x3 + 3x2 f”(x) = -3x2 + 6 f”'(x) = -6
2. lépés: Zérushelyek f(x) = 0 Horner-elrendezéssel N1 (0; 0) N2 (4; 0)
Metszéspontok a tengellyel: x = 0
Sy (0; 0)
3. lépés: Szélsőértékek: f'(x) = 0 -x3 + 3x2 = 0 ⇒ x1 = 0 x2 = 3 y1 = 0 y2 = 6,75 E1 (0; 0) = min E2 (3; 6,75) = max
Kérdés: maximum vagy minimum? f”(x) < o maximum f”(x) > o minimum f”(x1) = f”(0) = 6 > 0 minimum = min f”(x2) = f”(3) = -21 < 0 maximum = max
4. lépés: Inflexiós pont: f”(x) = 0 -3x2 + 6 = 0 x1 = √2 x2 = -√2 ⇒ y1 = f(x) = 1,82 y2 = f(x) = -3,82 W1(√2; 1,82) W2(-√2; -3,82)
Inflexiós pontba húzott érintő egyenlete: k = f'(x) k1 = f'(√2) = 3,17 k2 = f'(-√2) = 8,82 y – 1,82 = 3,17 . (x – √2) y1 = 3,17x – 2,66 y + 3,82 = -3,82 . (x + √2) y2 = -3,82x – 9,22
elrejt |
| 4.)
|
|
MEGOLDÁS 1. lépés: Deriváltak képzése
2. lépés: Zérushelyek f(x) = 0 Horner-elrendezéssel N1 (0; 0) N2 (-2√3; 0)
Metszéspontok a tengellyel: x = 0 y = 0 Sy (0; 0)
3. lépés: Szélsőértékek: f'(x) = 0
y1 = -4 y2 = 4 E1 (2; -4) = min E2 (-2; 4) = max
Kérdés: maximum vagy minimum? f”(x) < o maximum f”(x) > o minimum f”(x1) = f”(2) = 3 > 0 minimum = min f”(x2) = f”(-2) = -3 < 0 maximum = max
4. lépés: Inflexiós pont: f”(x) = 0
W(0; 0)
Inflexiós pontba húzott érintő egyenlete: k = f'(x) y – 0 = -3 . (x – 0) y = -3x
elrejt |
| 5.)
|
|
MEGOLDÁS 1. lépés: Deriváltak képzése
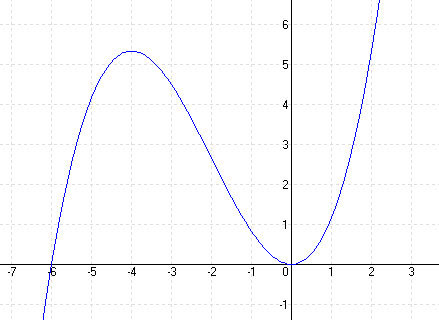
2. lépés: Zérushelyek f(x) = 0 Horner-elrendezéssel N1 (0; 0) N2 (-6; 0)
Metszéspontok a tengellyel: x = 0 y = 0 Sy (0; 0)
3. lépés: Szélsőértékek: f'(x) = 0
y1 = 0 y2 = 5,33 E1 (0; 0) = min E2 (-4; 5,33) = max
Kérdés: maximum vagy minimum? f”(x) < o maximum f”(x) > o minimum f”(x1) = f”(0) = 2 > 0 minimum = min f”(x2) = f”(-4) = -2 < 0 maximum = max
4. lépés: Inflexiós pont: f”(x) = 0 x + 2 = 0 x = -2 ⇒ y = f(x) = 2,66 W(-2; 2,66)
Inflexiós pontba húzott érintő egyenlete: k = f'(x) y – 2,66 = -6 . (x + 2) y = -6x – 9,34
elrejt |
| 6.) f(x) = x3 – 3x2 + 4 |
|
MEGOLDÁS 1. lépés: Deriváltak képzése
f'(x) = 3x2 – 6x f”(x) = -6x – 6 f”'(x) = 6
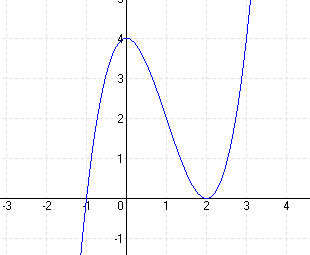
2. lépés: Zérushelyek f(x) = 0 Horner-elrendezéssel N1 (-1; 0) N2 (2; 0)
Metszéspontok a tengellyel: x = 0 y = 03 – 3 . 02 + 4 = 0 Sy (0; 4)
3. lépés: Szélsőértékek: f'(x) = 0 3x2 – 6x = 0 ⇒ x1 = 0 x2 = 2 y1 = 4 y2 = 0 E2 (2; 0) = min E1 (0; 4) = max
Kérdés: maximum vagy minimum? f”(x) < o maximum f”(x) > o minimum f”(x1) = f”(0) = -6 < 0 maximum = max f”(x2) = f”(2) = 6 > 0 minimum = min
4. lépés: Inflexiós pont: f”(x) = 0 6x – 6 = 0 x = 1 ⇒ y = f(x) = 2 W(1; 2)
Inflexiós pontba húzott érintő egyenlete: k = f'(x) y – 2 = -3 . (x – 1) y = -3x + 5
elrejt |
| 7.)
|
|
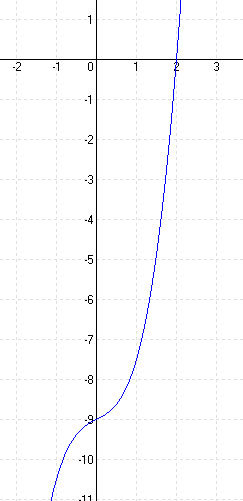
MEGOLDÁS 1. lépés: Deriváltak képzése
2. lépés: Zérushelyek f(x) = 0 Horner-elrendezéssel N1 (2; 0)
Metszéspontok a tengellyel: x = 0 y = -9 Sy (0; -9)
3. lépés: Szélsőértékek: f'(x) = 0
⇒ diszkrimináns < 0 nincs szélsőérték
4. lépés: Inflexiós pont: f”(x) = 0 6x = 0 x = 0 ⇒ y = f(x) = -9 W(0; -9)
Inflexiós pontba húzott érintő egyenlete: k = f'(x)
elrejt |
| 8.) f(x) = 2x3 – 6x2 + 6x |
|
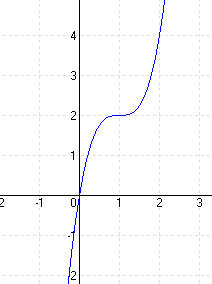
MEGOLDÁS 1. lépés: Deriváltak képzése
f'(x) = 6x2 – 12x + 6 f”(x) = 12x – 12 f”'(x) = 12
2. lépés: Zérushelyek f(x) = 0 Horner-elrendezéssel N1 (0; 0)
Metszéspontok a tengellyel: x = 0 y = 0 Sy (0; 0)
3. lépés: Szélsőértékek: f'(x) = 0 6x2 – 12x + 6 = 0 ⇒ x1 = x2 = 1 y = 2 E (1; 2) = inflexiós pont
Kérdés: maximum vagy minimum? f”(x) < o maximum f”(x) > o minimum f”(x) = f”(1) = 0 < 0 inflexiós pont
4. lépés: Inflexiós pont: f”(x) = 0 12x – 12 = 0 x = 1 ⇒ y = f(x) = 0 W(1; 0)
Inflexiós pontba húzott érintő egyenlete: k = f'(x) y – 0 = 0 . (x – 1) y = 0
elrejt |
| 9.)
|
| 10.)
|
|
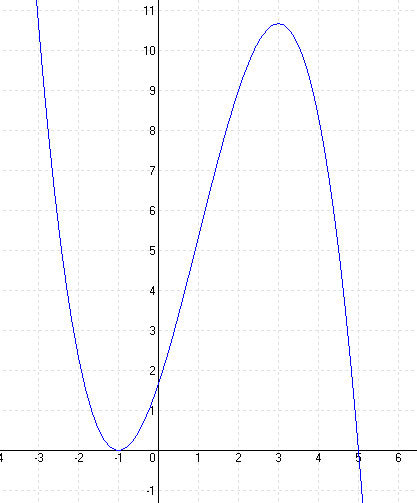
MEGOLDÁS 1. lépés: Deriváltak képzése
2. lépés: Zérushelyek f(x) = 0 Horner-elrendezéssel N1 (-1; 0) N2 (5; 0)
Metszéspontok a tengellyel: x = 0
3. lépés: Szélsőértékek: f'(x) = 0
⇒ x1 = 3 x2 = -1
Kérdés: maximum vagy minimum? f”(x) < o maximum f”(x) > o minimum f”(x1) = f”(3) = -4 < 0 maximum = max f”(x2) = f”(-1) = 4 > 0 minimum = min
4. lépés: Inflexiós pont: f”(x) = 0
x = 1 ⇒ y = f(x) = 6 W(1; 6)
Inflexiós pontba húzott érintő egyenlete: k = f'(x)
y – 6 = 4 . (x – 1) y = 4x + 2
elrejt |
| 11.)
|
|
MEGOLDÁS 1. lépés: Deriváltak képzése f'(x) = 0,6x2 + 0,6x – 1,2 f”(x) = 1,2x + 0,6 f”'(x) = 1,2
2. lépés: Zérushelyek f(x) = 0 Horner-elrendezéssel N1 (√6; 0) N2 (-1,5; 0) N3 (-√6; 0)
Metszéspontok a tengellyel: x = 0 y = -1,8 Sy (0; -1,8)
3. lépés: Szélsőértékek: f'(x) = 0 0,6x2 + 0,6x – 1,2 = 0 ⇒ x1 = 1 x2 = -2 y1 = -2,25 y2 = 0,2 E1 (1; -2,5) = min E2 (-2; 0,2) = max
Kérdés: maximum vagy minimum? f”(x) < o maximum f”(x) > o minimum f”(x1) = f”(1) = 1,8 > 0 minimum = min f”(x2) = f”(-2) = -1,8 < 0 maximum = max
4. lépés: Inflexiós pont: f”(x) = 0 1,2x + 0,6 = 0
Inflexiós pontba húzott érintő egyenlete: k = f'(x)
elrejt |
| 12.)
|
|
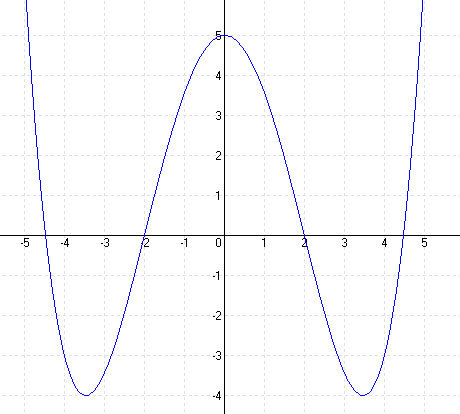
MEGOLDÁS 1. lépés: Deriváltak képzése f'(x) = 2x3 – 6x f”(x) = 6x2 – 6 f”'(x) = 12x
2. lépés: Zérushelyek f(x) = 0 Horner-elrendezéssel N1 (√3; 0) N2 (-√3; 0)
Metszéspontok a tengellyel: x = 0 y = 4,5 Sy (0; 4,5)
3. lépés: Szélsőértékek: f'(x) = 0 2x3 – 6x = 0 ⇒ x1 = 0 x2 = √3 x3 = -√3 y1 = 4,5 y2 = 0 y3 = 0 E1 (0; 0) = max E2 (√3; 0) = min E3 (-√3; 0) = min
Kérdés: maximum vagy minimum? f”(x) < o maximum f”(x) > o minimum f”(x1) = f”(0) = -6 < 0 maximum = max f”(x2) = f”(√3) = 12 > 0 minimum = min f”(x3) = f”(-√3) = 12 > 0 minimum = min
4. lépés: Inflexiós pont: f”(x) = 0 6x2 – 6 = 0 x1 = 1 x2 = -1 ⇒ y1 = f(x1) = 2 y2 = f(x2) = 2 W1(1; 2) W2(-1; 2)
Inflexiós pontba húzott érintő egyenlete: k = f'(x) y1 – 2 = -4 * (x – 1) y2 – 2 = 4 * (x + 1) y1 = -4x + 6 y2 = 4x + 6
elrejt |
| 13.)
|
|
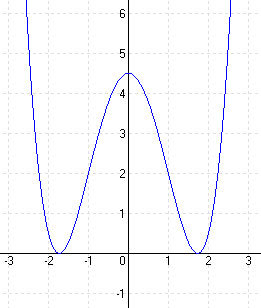
MEGOLDÁS 1. lépés: Deriváltak képzése
2. lépés: Zérushelyek f(x) = 0 Horner-elrendezéssel N1 (2; 0) N2 (-2; 0)
Metszéspontok a tengellyel: x = 0 y = 5 Sy (0; 5)
3. lépés: Szélsőértékek: f'(x) = 0
y1 = 5 y2 = -4 y3 = -4 E1 (0; 5) = max E2 (√12; -4) = min E3 (-√12; -4) = min
Kérdés: maximum vagy minimum? f”(x) < o maximum f”(x) > o minimum f”(x1) = f”(0) = -3 < 0 maximum = max f”(x2) = f”(√12) = 6 > 0 minimum = min f”(x3) = f”(-√12) = 6 > 0 minimum = min
4. lépés: Inflexiós pont: f”(x) = 0
x1 = 2 x2 = -2 ⇒ y1 = f(x1) = 2 y2 = f(x2) = 2 W1(2; 0) W2(-2; 0)
Inflexiós pontba húzott érintő egyenlete: k = f'(x) y1 – 0 = 2 * (x – 2) y2 – 0 = -2 * (x + 2) y1 = 2x – 4 y2 = -2x – 4
elrejt |
![\[x_{1;2} = \frac{1 \pm \sqrt{-1^2 - 4 * -2}}{2 * 1} = \frac{1 \pm \sqrt{9}}{2} =\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-a6cfa5d285d381a0649f5fd39e89f999_l3.png "Rendered by QuickLaTeX.com")
![\[= \frac{1 \pm 3}{2} = \hspace{5}\rightarrow \hspace{5} x_1 = 2\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-85b774b1efc932137a9bd9c3c9586fea_l3.png "Rendered by QuickLaTeX.com")
![\[\hspace{140} \searrow \hspace{5}x_2 = -1\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-d44d4975377548f3ab0f877750618bee_l3.png "Rendered by QuickLaTeX.com")
![\[= 2x - 1 = 0\hspace{25} \Rightarrow \hspace{10} x =\frac{1}{2}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-48208904d03baebb4ca0ee85e2355d72_l3.png "Rendered by QuickLaTeX.com")
![\[y = (\frac{1}{2})^2 - \frac{1}{2} - 2 = \frac{1}{4} - \frac{1}{2} - 2 = \frac{1}{4} - \frac{2}{4} - 2 = 2,25\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-bc83d1cbd4a9d4ddec082f9bd4f8aaae_l3.png "Rendered by QuickLaTeX.com")
![\[ E (\frac{1}{2} ; 2,25)\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-55c7b3dca3a87523795db9cdbd4a5446_l3.png "Rendered by QuickLaTeX.com")
![\[ f''(\frac{1}{2}) = 2 \hspace{25} > o \hspace{10} minimum\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-82ae6ac8a8c4b5145a37a03404917522_l3.png "Rendered by QuickLaTeX.com")
![\[ x = \frac{1}{2} \hspace{20}\Rightarrow y = f(x) = 3\frac{1}{8}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-da19dc32885c27f183e09b0665cc5a91_l3.png "Rendered by QuickLaTeX.com")
![\[ W(\frac{1}{2}; 3\frac{1}{8})\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-dac665bf7b1a879e16c1b0c853bddfc6_l3.png "Rendered by QuickLaTeX.com")
![\[ y - 3\frac{1}{8} = \frac{15}{4}* (x - \frac{1}{2}) = \frac{15}{4}x + \frac{10}{8}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-11a3e80c5fe2adc433bf25318b9c9e3f_l3.png "Rendered by QuickLaTeX.com")
![\[f(x) = -\frac{x^4}{4} + x^3\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-67956fd3d0fe33e0486157c784b3497c_l3.png "Rendered by QuickLaTeX.com")
![\[y = -\frac{0^4}{4} + 0^3 = 0\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-23c7cd696221bdcac112adbf8a545ce9_l3.png "Rendered by QuickLaTeX.com")
![\[f(x) = -\frac{x^3}{4} - 3x\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-bf33413b542a3f328909244a8cb6b38a_l3.png "Rendered by QuickLaTeX.com")
![\[f'(x) = \frac{3}{4}x^2 - 3\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-109a586398ed45a37889f2dc5b8cee24_l3.png "Rendered by QuickLaTeX.com")
![\[f''(x) = \frac{3}{2}x\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-041cb6db7d5353e03dab87b4b8684ed4_l3.png "Rendered by QuickLaTeX.com")
![\[f'''(x) = \frac{3}{2}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-58f0bf27cabce8ef79e482a32db3a594_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{3}{4}x^2 - 3 = 0 \Rightarrow \hspace{30} x_1 = 2 \hspace{15} x_2 = -2\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-a692e5ab8fa3183b5833f5129af281d6_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{3}{2}x = 0 \hspace{30} x = 0 \hspace{30}\Rightarrow y = f(x) = 0\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-10312cc4e27f2235dfbf8faeb0095fd8_l3.png "Rendered by QuickLaTeX.com")
![\[f(x) = -\frac{x^3}{6} + x^2\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-6a8433181ed1b78f6860632216517c10_l3.png "Rendered by QuickLaTeX.com")
![\[f'(x) = \frac{1}{2}x^2 + 2x\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-a05daad4e10f981cf195190a042386ed_l3.png "Rendered by QuickLaTeX.com")
![\[f''(x) = x + 2\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-360d5373376669fc64ac7f7badf40fec_l3.png "Rendered by QuickLaTeX.com")
![\[f'''(x) = 1\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-9628d2f2018c75f5fb28b146cb229128_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{1}{2}x^2 + 2x = 0 \Rightarrow \hspace{30} x_1 = 0 \hspace{15} x_2 = -4\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-eb9d0be441b83f7a392d3911cfd70e9e_l3.png "Rendered by QuickLaTeX.com")
![\[f(x) = x^3 + \frac{x}{2} - 9\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-fd998b32db10ed575233626f503e8317_l3.png "Rendered by QuickLaTeX.com")
![\[f'(x) = 3x^2 + \frac{1}{2}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-a0a0c7314ab43af05d8160bdcec0f461_l3.png "Rendered by QuickLaTeX.com")
![\[f''(x) = 6x\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-61c330279cb024c1b011d5d298c3b01c_l3.png "Rendered by QuickLaTeX.com")
![\[f'''(x) = 6\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-d46b88d240c19a7eaeb6a4a66a7707b5_l3.png "Rendered by QuickLaTeX.com")
![\[3x^2 + \frac{1}{2} = 0 \]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-255cfc7ebed783b1edf9deb38f4300cc_l3.png "Rendered by QuickLaTeX.com")
![\[y + 9 = \frac{1}{2} * (x - 0) \]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-64d61a69d10c0995409acd41094ec758_l3.png "Rendered by QuickLaTeX.com")
![\[y = \frac{1}{2}x - 9 \]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-dee46a3a5ad1b78338a6ac186c174775_l3.png "Rendered by QuickLaTeX.com")
![\[f(x) = \frac{1}{4} * (x^3 - 3x^2 - 9x + 27)\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-f759f8ab75859988ad1ebe52f4997d1f_l3.png "Rendered by QuickLaTeX.com")
![\[f(x) = \frac{1}{3} * (-x^3 + 3x^2 + 9x + 5)\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-d803345df94dfa0583e1f5e47bd5b234_l3.png "Rendered by QuickLaTeX.com")
![\[f'(x) = \frac{1}{3} * (-3x^2 + 6x + 9) \]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-eb1815cd215985a5737be2c7ae249ee1_l3.png "Rendered by QuickLaTeX.com")
![\[f''(x) = \frac{1}{3} * (-6x + 6)\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-004cbe6b87b9ce7caaf630c293dfe6cc_l3.png "Rendered by QuickLaTeX.com")
![\[f'''(x) = \frac{1}{3} * -6 = -2\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-596a229dcfb5ab7612f5d2b585ffb5f0_l3.png "Rendered by QuickLaTeX.com")
![\[ y = \frac{5}{3}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-3694d58b34a6ae86e41d40986d1cfa64_l3.png "Rendered by QuickLaTeX.com")
![\[ S_y (0; \frac{5}{3})\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-7d1adf620ef98131c46a759545ca5911_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{1}{3} * (-3x^2 + 6x + 9) = 0 \]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-be85ceca3c89a530a1d23aac5b4d4b16_l3.png "Rendered by QuickLaTeX.com")
![\[y_1 = \frac{32}{3} \hspace{25} y_2 = 0 \]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-98a1f3a9d17f389ef8f60d509f0f2fd8_l3.png "Rendered by QuickLaTeX.com")
![\[E_1 (3;\frac{32}{3}) = max \hspace{25} E_2 (-1; 0) = min \]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-36b4663fecf48927bf451f40ee2c8d9e_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{1}{3} * (-6x + 6 = 0) \]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-1209e77302843ea4a0da29fc09d344ea_l3.png "Rendered by QuickLaTeX.com")
![\[f(x) = \frac{1}{10} * (2x + 3) * (x^2 - 6)\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-bdc2166f4d8dfcead7bd2c4c8a83fd70_l3.png "Rendered by QuickLaTeX.com")
![\[ x = -\frac{1}{2} \hspace{20}\Rightarrow y = f(x) = -1,15\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-177046895ae9cebe9922e9175d3bcac5_l3.png "Rendered by QuickLaTeX.com")
![\[ W(-\frac{1}{2}; -1,15)\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-08af2fc6ff48497146c632a08af7a48a_l3.png "Rendered by QuickLaTeX.com")
![\[ y + 1,15 = -1,35 * (x + \frac{1}{2}) \hspace{25}y = 1,35x - 1,825\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-3edc06443daabe31b4243be7c90d79d1_l3.png "Rendered by QuickLaTeX.com")
![\[f(x) = \frac{1}{2} * (x^4 - 6x^2 + 9)\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-38511b96fc2aff864ad2e94e841b0b85_l3.png "Rendered by QuickLaTeX.com")
![\[f(x) = \frac{x^4}{16} - \frac{3x^2}{2} + 5)\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-8cb4f78d43d17eb119569f733d4704ea_l3.png "Rendered by QuickLaTeX.com")
![\[f'(x) = \frac{1}{4}x^3 - 3x\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-94b129705291a32663e0a26d032c987e_l3.png "Rendered by QuickLaTeX.com")
![\[f''(x) = \frac{3}{4}x^2 - 3\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-ac4d46112e6fde2507b6158c02ab47b5_l3.png "Rendered by QuickLaTeX.com")
![\[f'''(x) = \frac{3}{2}x\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-008879476d3698de4322b942e0b27024_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{1}{4}x^3 - 3x = 0 \Rightarrow \hspace{30} x_1 = 0 \hspace{15} x_2 = \sqrt{12} \hspace{15}x_3 = -\sqrt{12}\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-ebbc9411aaa028413c544d807d0fddbc_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{3}{4}x^2 - 3 = 0\]](https://tudomanyplaza.hu/wp-content/ql-cache/quicklatex.com-4c18799f349e8df1f5dfe18061e979a4_l3.png "Rendered by QuickLaTeX.com")
A függvényképek helyesek, de előfordulhat, hogy az eredményeket elszámoltam. Ha így lenne, kérlek, jelezd a hibát a hibás feladatot!
No Comment